3.1. Анализ преобразований
Преобразования арифметических корней осуществляются посредством приведенных ниже основных свойств.
1. Если 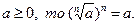
2. При любом значении а 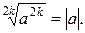
3. Если 
4. Если 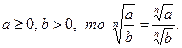
5. Если 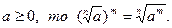
6. Если 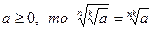
7. Если 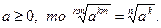
Проанализируем перечисленные свойства с позиции их влияния на область допустимых значений переменных а и в,если не ограничиваться рассмотрением их неотрицательных значений значений.
Свойство 1: 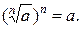
Рассмотрим чётные значения показателя корня п =2 k, 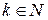 . Тогда область определения левой части равенства есть множество неотрицательных действительных чисел. В правой части равенства допустимыми являются любые значения а. Следовательно, использование свойства 1 слева направо приводит к расширению области определения, а справа налево – к её сужению, что при решении уравнений может способствовать приобретению посторонних корней или их потере.
. Тогда область определения левой части равенства есть множество неотрицательных действительных чисел. В правой части равенства допустимыми являются любые значения а. Следовательно, использование свойства 1 слева направо приводит к расширению области определения, а справа налево – к её сужению, что при решении уравнений может способствовать приобретению посторонних корней или их потере.
Чтобы не происходило изменения области определения при использовании свойства 1 слева направо, следует рассматривать систему
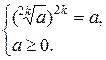
Справа налево свойство 1 фактически даёт возможность представить число а в виде корня п – ой степени. Например, число 2 представимо как 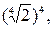 а число -2 как
а число -2 как 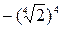 .
.
В общем виде, если п – чётное число, то
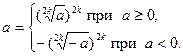
Отметим, что свойство (1) используется при внесении множителя под знак корня.
Ясно, что если п – нечётное число, то изменения области определения при использовании свойства 1 не происходит.
Проиллюстрируем применение свойства (1) в процессе решения уравнений.
Пример 1. Решить уравнение 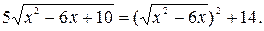
Воспользовавшись свойством 1, заменим данное уравнение равносильной ему системой
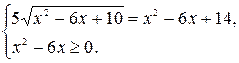
Решим уравнение системы. Введём замену 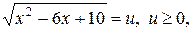 тогда
тогда 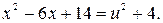 Уравнение примет вид
Уравнение примет вид 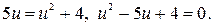 Полученное уравнение имеет корни 1 или 4. Следовательно,
Полученное уравнение имеет корни 1 или 4. Следовательно, 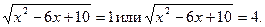 Первое уравнение имеет корень 3, а второе -
Первое уравнение имеет корень 3, а второе - 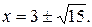
Рассмотрим решение неравенства системы.

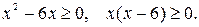
 .
.
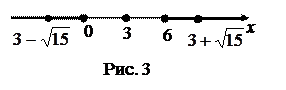 Наконец, решим систему:
Наконец, решим систему:
Ответ: 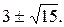
Пример 2. Решить уравнение 
 Установим область определения данного уравнения. Она задаётся неравенством
Установим область определения данного уравнения. Она задаётся неравенством 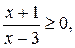 решая которое получим
решая которое получим
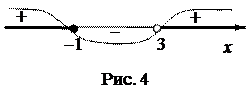
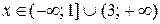 .
.
Представим в области определения выражение х – 3 в виде квадратного корня:
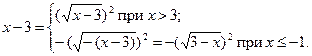
Данное уравнение равносильно совокупности двух систем
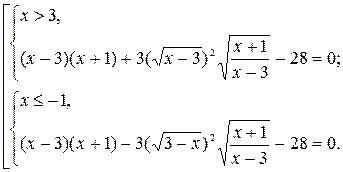
Далее используем свойство 5:
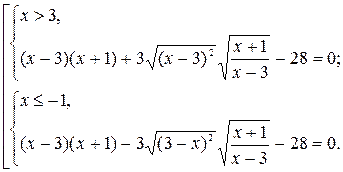
Учитывая, что 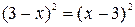 , и применяя свойство 2, получим
, и применяя свойство 2, получим
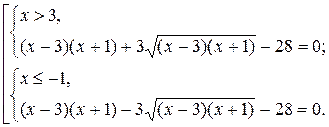
(1)
(2)
Решим уравнение системы (1), введя замену  Оно примет вид
Оно примет вид 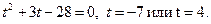 Отсюда
Отсюда 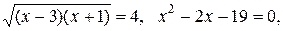
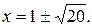 Неравенству
Неравенству 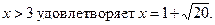
Решая уравнение второй системы аналогично, получим t = 7 или t =-4. Тогда 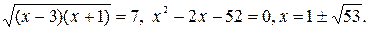 Неравенству системы
Неравенству системы 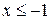 удовлетворяет корень
удовлетворяет корень 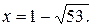
Ответ: 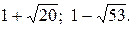
Свойство 2: при любом значении а 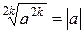
Рассмотрим свойство 2 на примере выражения 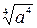 . Данный арифметический (неотрицательный) корень определён при любом значении а. Если записать, что
. Данный арифметический (неотрицательный) корень определён при любом значении а. Если записать, что 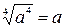 , то допустимые значения а в правой части равенства по определению арифметического корня могут быть только неотрицательными (
, то допустимые значения а в правой части равенства по определению арифметического корня могут быть только неотрицательными (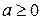 ), то есть происходит сужение области допустимых значений переменной а. Следовательно, необходимо рассмотреть значения данного выражения и для отрицательных значений а:если
), то есть происходит сужение области допустимых значений переменной а. Следовательно, необходимо рассмотреть значения данного выражения и для отрицательных значений а:если 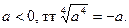 Так как рассмотренные равенства совпадают с определение модуля числа, то второе свойство может быть записано в виде
Так как рассмотренные равенства совпадают с определение модуля числа, то второе свойство может быть записано в виде
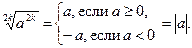
Не рассматривая эти два случая, мы ограничиваем область допустимых значений переменной а, что в процессе решения уравнений может привести к потере корней.
Приведём примеры использования свойства 2 в процессе решения уравнений.
Пример 3. Решить уравнение 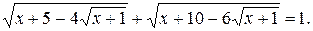
Введём замену 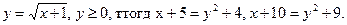 Данное уравнение примет вид
Данное уравнение примет вид 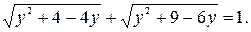
Далее  По свойству 2 полученное уравнение равносильно уравнению
По свойству 2 полученное уравнение равносильно уравнению 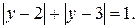 Решим его методом интервалов.
Решим его методом интервалов.
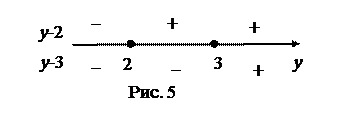
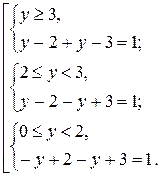
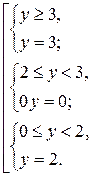
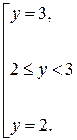
Таким образом, 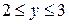 . Тогда
. Тогда 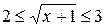 , 3 £ х £8.
, 3 £ х £8.
Ответ: [3;8]
Пример 4. Решить уравнение 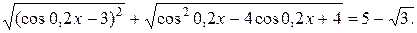
Решение: 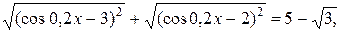
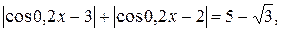
Учитывая свойство ограниченности функции косинус значениями -1 и 1, воспользуемся второй строчкой в записи свойства 2. Получим
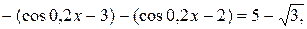
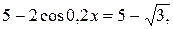
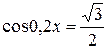 ,
, 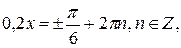
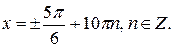
Ответ: 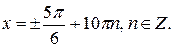
Пример 5. Решить уравнение 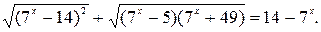
Используя свойство 2, выполним тождественное преобразование, не меняющее области определения данного уравнения. Получим уравнение 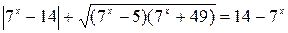 , равносильное данному. Так как в левой части данного уравнения записана сумма арифметических корней, то выражение в правой части уравнения должно удовлетворять неравенству 14-7 х ³ 0. Тогда, раскрывая модуль, придём к уравнению
, равносильное данному. Так как в левой части данного уравнения записана сумма арифметических корней, то выражение в правой части уравнения должно удовлетворять неравенству 14-7 х ³ 0. Тогда, раскрывая модуль, придём к уравнению 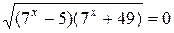 . Его корень
. Его корень 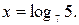
Ответ: 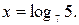
Свойство 3: 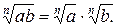
Рассмотрим равенство 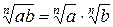 при чётных значениях п (n=2k, kÎN). Допустимые значения переменных в левой части формулы удовлетворяют неравенству ав ≥ 0, то есть принимают значения одного знака. Допустимые значения переменных а и в в правой части формулы удовлетворяют неравенствам а ≥ 0 и в ≥ 0. Таким образом, применение свойства (2) в процессе решения уравнения «слева направо» приводит к сужению области определения уравнения и, возможно, к потере корней, а «справа налево» к расширению области определения уравнения и, возможно, к появлению посторонних корней.
при чётных значениях п (n=2k, kÎN). Допустимые значения переменных в левой части формулы удовлетворяют неравенству ав ≥ 0, то есть принимают значения одного знака. Допустимые значения переменных а и в в правой части формулы удовлетворяют неравенствам а ≥ 0 и в ≥ 0. Таким образом, применение свойства (2) в процессе решения уравнения «слева направо» приводит к сужению области определения уравнения и, возможно, к потере корней, а «справа налево» к расширению области определения уравнения и, возможно, к появлению посторонних корней.
В связи с выше сказанным, свойство 2 используется в виде
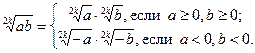 (2.1.)
(2.1.)
В этом случае область допустимых значений переменных не изменяется. Иногда свойство (2) используется в виде 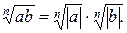 (2.2.) Однако его применение в такой форме не сохраняет область определения уравнения, а расширяет её. Проиллюстрируем сказанное на примере.
(2.2.) Однако его применение в такой форме не сохраняет область определения уравнения, а расширяет её. Проиллюстрируем сказанное на примере.
Пример 6. Решить уравнение 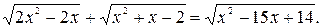
Установим область определения данного уравнения. Составим и решим систему неравенств.
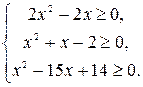
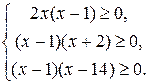

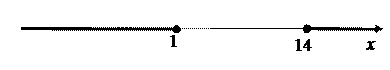
Область определения данного уравнения D = (-¥; -2] È {1} È [14;+¥).
При х Î D данное уравнение равносильно уравнению
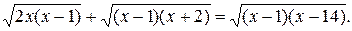 (*)
(*)
Воспользуемся свойством (2). Получим
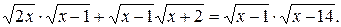
Выполненное преобразование сузило область определения данного уравнения до значений х Î [14;+¥), что может привести к потере корней. Поэтому необходимо рассмотреть два случая.
1) При х Î [14;+¥) каждый множитель в подкоренных выражениях уравнения (*) положителен.Воспользуемся первой строчкой в записи свойства 2.
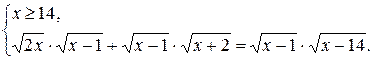
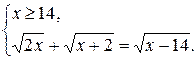
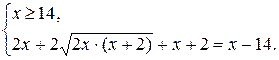
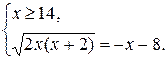
Очевидно, что полученная система решений не имеет.
2) При х Î (-¥; -2] каждый множитель в подкоренных выражениях уравнения (*) отрицателен. Воспользуемся второй строчкой в записи свойства 2.

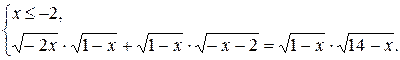
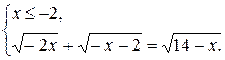
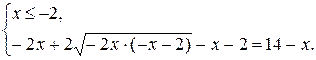
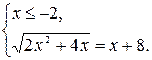
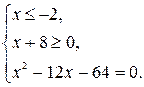

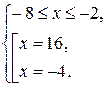
х = - 4 – решение системы (корень уравнения).
Очевидно, что х = 1 также является корнем данного уравнения.
Ответ: -4; 1.
Применение свойства 2 в виде 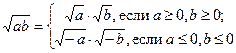
можно условно назвать «по двум дорожкам».
Замечание. Чтобы преобразование корней не сузило область определения данного уравнения и не привело к потере корней, можно использовать свойство 2 в форме 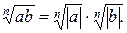 Тогда уравнение запишется в виде
Тогда уравнение запишется в виде
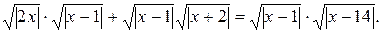
Далее, с учётом области определения, уравнение сведётся к рассмотрению двух случаев, приведённых выше. Раскрывая модуль при х Î [14;+¥), получим уравнение 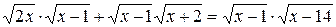 ,
,
а при при х Î (-¥;-2] - уравнение 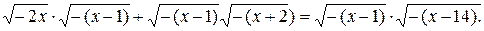
Пример 7. Решить систему уравнений 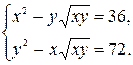
Решение данной системы предполагает вынесение за скобки общих множителей. В первом уравнении 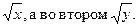 Выполнение такого преобразования основано на использовании свойства 2 в виде
Выполнение такого преобразования основано на использовании свойства 2 в виде
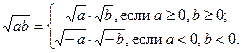 (2.1.)
(2.1.)
Заметим сразу, что х = 0, у = 0 не являются решением системы.
Если x >0, y >0, то получим 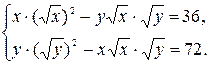
Если x <0, y <0, то получим 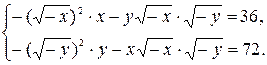
Решим первую систему.
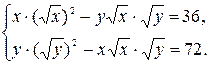
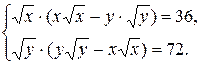
В результате деления первого уравнения на второе уравнение системы получим 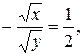 которое не имеет решений.
которое не имеет решений.
Решим вторую систему.
Если x <0, y <0, то 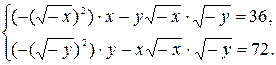
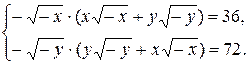
В результате деления первого уравнения на второе уравнение системы получим 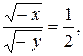
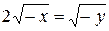 .
.
Составим равносильную систему:
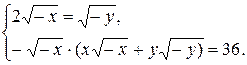
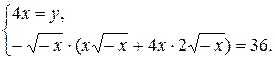
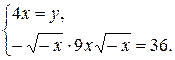
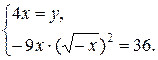
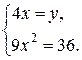
Учитывая, что x <0, y <0, получим х = - 2, у = - 8. Ответ: (- 2;- 8)
Свойство 4: 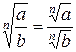
Аналогичные рассуждения при чётных значениях п приводят к необходимости представить свойство 4 в двух формах:
4.1. 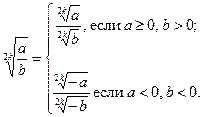 4.2.
4.2. 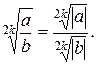
Приведём пример уравнения, при решении которого используется свойство 4. Рассмотрим три способа его решения.
Пример 8. Решить уравнение 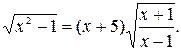
Первый способ.
Установим область определения данного уравнения D, решив неравенство 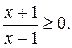 D = (- ¥; - 1] È (1;+¥).
D = (- ¥; - 1] È (1;+¥).
Ясно, что используя свойства 2 и 3 для представления данного уравнения в виде  мы сужаем область его определения до промежутка (1;+¥). Воспользуемся приёмом «по двум дорожкам». Тогда данное уравнение равносильно совокупности двух систем:
мы сужаем область его определения до промежутка (1;+¥). Воспользуемся приёмом «по двум дорожкам». Тогда данное уравнение равносильно совокупности двух систем:
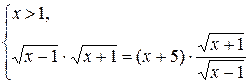
или
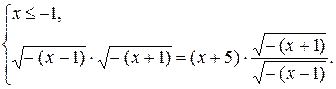
Решая первую систему, получим  Так как уравнение системы не имеет решений (оно сведётся к уравнению х – 1 = х + 5), то и система не имеет решений.
Так как уравнение системы не имеет решений (оно сведётся к уравнению х – 1 = х + 5), то и система не имеет решений.
Очевидно, что х = -1 является решением второй системы, поэтому её можно записать в виде
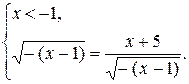 Решим уравнение системы: - х + 1 = х +5, х = - 2.
Решим уравнение системы: - х + 1 = х +5, х = - 2.
- 2 – решение системы. Ответ: -1; - 2.
Второй способ.
Воспользуемся формулой 3.2.
Получим 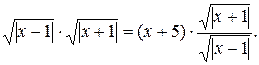 Область определения данного
Область определения данного
уравнения расширилась, следовательно, ожидаемы посторонние решения. Очевидно, что -1 – корень как полученного, так и данного уравнения. Решим уравнение 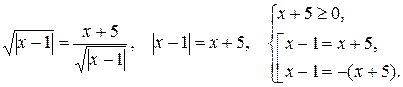
Получаем х = -2 – решение системы. Проверкой убеждаемся, что -2 – корень данного уравнения.
Третий способ.
Выполним преобразование, состоящее в приведении знаменателя к рациональному виду, получим 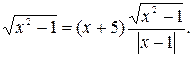 Замечательная особенность полученного уравнения состоит в том, что оно имеет такую же область определения как и данное. Его решение сведётся к совокупности двух уравнений
Замечательная особенность полученного уравнения состоит в том, что оно имеет такую же область определения как и данное. Его решение сведётся к совокупности двух уравнений 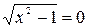 или
или 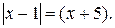 Первое уравнение имеет единственный корень, принадлежащий области определения, -1, а второе решено выше. Его корень - 2.
Первое уравнение имеет единственный корень, принадлежащий области определения, -1, а второе решено выше. Его корень - 2.
Ответ: -2; - 1.
Рассмотрим ещё один пример.
Пример 9. Решить уравнение 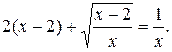
Область определения: D = (- ¥; 0) È [2;+¥).
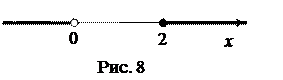
Отметим, что возможно решение каждым из трёх рассмотренных выше способов. Воспользуемся третьим способом, как наиболее простым.
В области определения данное уравнение равносильно уравнению
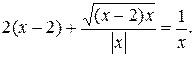 Исходя из определения модуля, получим совокупность двух систем:
Исходя из определения модуля, получим совокупность двух систем:
1) 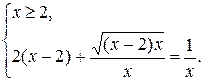
Уравнение системы посредством замены 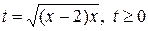 сведётся к квадратному
сведётся к квадратному 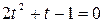 , неотрицательным решением которого является
, неотрицательным решением которого является 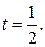 Тогда решением системы
Тогда решением системы 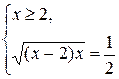 будет число
будет число 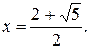
2) 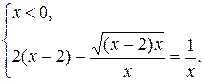
Решая уравнение аналогично, получим решение системы 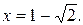
Итак, данное уравнение имеет решения 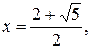
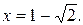
Ответ: 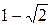 ;
; 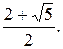
Свойство 5: 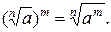
Применение свойства 5 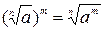 при четных значениях n и m может привести к расширению или сужению области определения уравнения и, как следствие, к потере или появлению посторонних корней. Так, область допустимых значений переменной а в выражении
при четных значениях n и m может привести к расширению или сужению области определения уравнения и, как следствие, к потере или появлению посторонних корней. Так, область допустимых значений переменной а в выражении 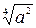 есть множество всех действительных чисел, а в выражении
есть множество всех действительных чисел, а в выражении 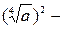 множество неотрицательных чисел. Поэтому для чётных значений показателей корня и степениданное свойство целесообразно записать в виде
множество неотрицательных чисел. Поэтому для чётных значений показателей корня и степениданное свойство целесообразно записать в виде 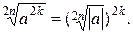
Проиллюстрируем на примере влияние свойства 5 на процесс решения уравнений.
Пример 10. Решить уравнение 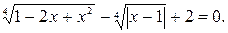
Представим данное уравнение в виде 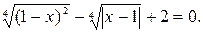 Область определения данного уравнения – множество всех действительных чисел R. Применяя свойство 5 в форме, не меняющей области определения уравнения, получим,
Область определения данного уравнения – множество всех действительных чисел R. Применяя свойство 5 в форме, не меняющей области определения уравнения, получим, 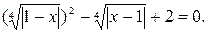 Ведение замены
Ведение замены 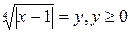 сведёт данное уравнение к квадратному
сведёт данное уравнение к квадратному 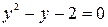 , имеющему корни -1 и 2. Тогда
, имеющему корни -1 и 2. Тогда 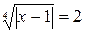 ,
, 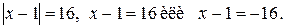 Получаем корни уравнения: 17, -15.
Получаем корни уравнения: 17, -15.
Ответ: -15; 17.
Свойство 6: 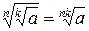
Проанализируем влияние свойства 6 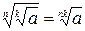 на область определения уравнения.
на область определения уравнения.
| Значения n | Значения k | Допустимые значения а в левой части равенства | Допустимые значения а в левой части равенства |
| Чётное | Чётное | Неотрицательные | Неотрицательные |
| Чётное | Нечётное | Неотрицательные | Неотрицательные |
| Нечётное | Чётное | Неотрицательные | Неотрицательные |
| Нечётное | Нечётное | Любые | Любые |
Таким образом, использование свойства 6 область допустимых значений переменной не меняет, но необходимо в первых трёх случаях её учитывать.
Свойство 7: 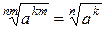
Рассмотрим применение свойства 7 на примерах выражений 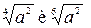 . Свойство 7 позволяет разделить показатель степени и показатель корня на одно и то же число. Тогда получим
. Свойство 7 позволяет разделить показатель степени и показатель корня на одно и то же число. Тогда получим 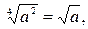
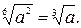 В первом равенстве
В первом равенстве 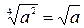 левая и правая части имеют разные области определения. Чтобы спасти ситуацию, перепишем его в виде
левая и правая части имеют разные области определения. Чтобы спасти ситуацию, перепишем его в виде 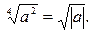 Во втором равенстве
Во втором равенстве 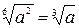 области определения совпадают, однако, левая часть принимает при
области определения совпадают, однако, левая часть принимает при 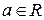 неотрицательные значения, а правая как неотрицательные (при
неотрицательные значения, а правая как неотрицательные (при 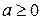 ), так и отрицательные значения
), так и отрицательные значения 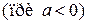 . Поэтому
. Поэтому 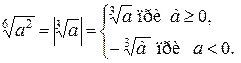
В общем виде: 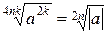 ,
, 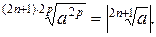
Приведём примеры использования свойства 7 в процессе решения уравнений.
Пример 11. Решить систему уравнений 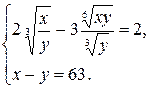
В соответствии со свойством 7 преобразуем выражение 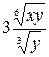 .
.
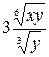 =
= 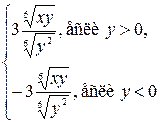 =
= 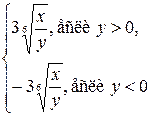
Данная система равносильна совокупности двух систем
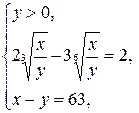 или
или 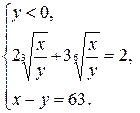
Вводя замену 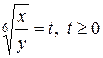 в первом уравнении, получим
в первом уравнении, получим 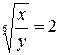 . Решением первой систему будет пара чисел (64; 1).
. Решением первой систему будет пара чисел (64; 1).
Решая аналогично вторую систему, получим ещё одну пару чисел, удовлетворяющих системе (-1; -64).
Ответ: (64; 1), (-1; -64).
Пример 12. Решить уравнение 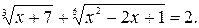
Преобразуя левую часть данного уравнения, получим 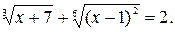 По свойству 7 данное уравнение равносильно уравнению
По свойству 7 данное уравнение равносильно уравнению 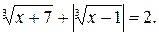 Введём замену
Введём замену 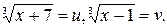
Данное уравнение сведётся к системе 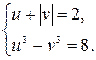
Решая 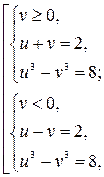 получим
получим 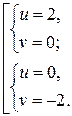
Тогда 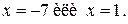
Ответ: - 7; 1.
Пример 13. Решить уравнение 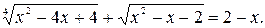 Преобразуем
Преобразуем 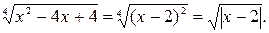 Так как в левой части уравнения содержится сумма двух арифметических корней, то выражение 2 - х удовлетворяет условию
Так как в левой части уравнения содержится сумма двух арифметических корней, то выражение 2 - х удовлетворяет условию 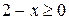 , то есть
, то есть 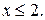 Тогда
Тогда 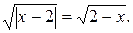
Рассмотрим выражение 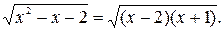 Так как
Так как 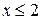 , то
, то 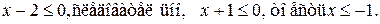
Тогда 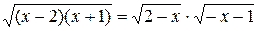 . Наконец, представим, используя свойство 1,
. Наконец, представим, используя свойство 1, 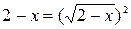 . Данное уравнение равносильно системе
. Данное уравнение равносильно системе 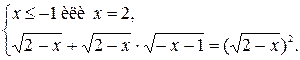
Очевидно, что х= 2 – корень уравнения и решение системы. Перепишем систему в виде 
Решим уравнение системы 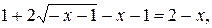
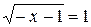 ,
, 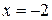 .
.
-2 – решение системы.
Ответ: -2; 2.
3.2. Комплекс заданий
Решить уравнение. Ответ.
№ 1. 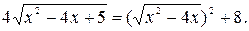
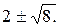
№ 2. 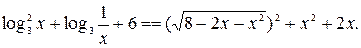
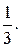
№ 3. 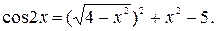
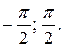
№ 4. 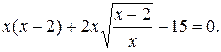
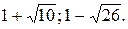
№ 5. 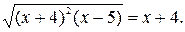 -4; 6.
-4; 6.
№ 6. 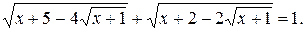 [0;3].
[0;3].
№ 7. 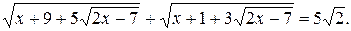 4.
4.
№ 8. 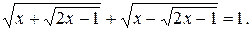 Нет решений.
Нет решений.
№ 9. 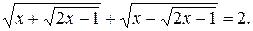 1,5.
1,5.
№ 10. 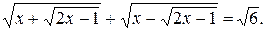 [3;+¥).
[3;+¥).
№ 11. 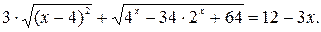 1.
1.
№ 12. 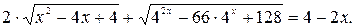 0,5.
0,5.
№ 13. 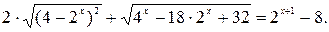 4.
4.
№ 14. 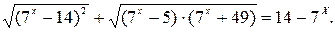
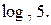
№ 15. 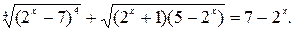
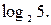
№ 16. 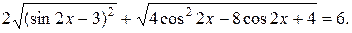
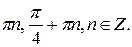
№ 17. 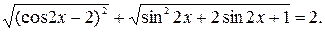
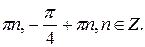
№ 18. 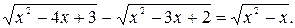
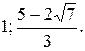
№ 19. 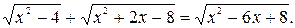
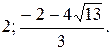
№ 20. 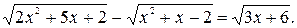
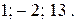
№ 21. 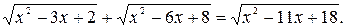
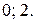
№ 22. 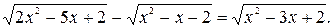
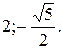
№ 23. 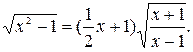 -1; 4.
-1; 4.
№ 24. 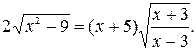 -3; 11.
-3; 11.
№ 25. 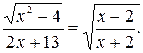 -5; 2.
-5; 2.
№ 26. 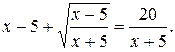

№ 27. 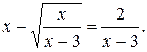
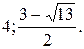
№ 28. 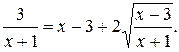
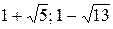 .
.
№ 29. 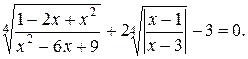 2.
2.
№ 30. 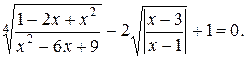 2.
2.
№ 31. 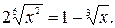
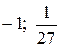 .
.
№32. Решить систему уравнений 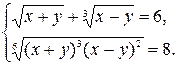
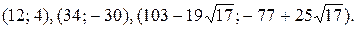
Приведём таблицу использования свойств корней при решении уравнений составленного комплекса.
| Номера свойств | ||||||
| Номера заданий | 1 - 4 | 5 - 17 | 18 - 22 | 23 - 28 | 30 - 32 |






