Варіант 1
Початковий рівень
1. Коренем рівняння - х = 15 є число...
а) -15; б) -3; в) 3; г) 15.
2. У якому випадку доданок 7 х правильно перенесений з однієї частини рівняння 3 х = 7 х + 42 в іншу?
а) 3 х - 7 х = 42; б) 3 х + 7 х = 42; в) -3 х + 7 х = 42; г) -3 х - 7 х = 42.
3. Одне з чисел на 7,5 більше від іншого. Якщо менше з чисел позначити
через х, то більше з чисел дорівнюватиме...
а) х + 7,5; б) х - 7,5; в) 7,5 - х; г) 7,5 х.
4. Марійка прочитала на 20 сторінок менше, ніж Сергій. Якщо кількість сторінок, які прочитала Марійка, позначити через х, то Сергій прочитав...
а) 20 х; б) х + 20; в) х - 20; г) х: 20.
Середній рівень
1.У якому випадку у рівнянні х + 5 = 7 - 4 х правильно перенесено всі до
данки, які містять невідоме, у ліву частину, а доданки, які не містять не
відомого, — у праву?
а) х - 4 х = 7 + 5; б) - х + 4 х = -7 + 5;
в) х + 4 х = 7 + 5; г) х - 4 х = 7-5.
2.В одній папці було зошитів у 2 рази більше, ніж у другій. Якщо з
першої папки перекласти в другу 16 зошитів, то в обох папках стане
порівну. Скільки зошитів було в другій папці?
Яке з рівнянь а-г відповідає умові задачі, якщо через х позначено
кількість зошитів у другій папці?
а) 
б) 
в) 
г) 
3. Перше число утричі менше від другого. Якщо до першого числа додати 3,7, а від другого відняти 5,3, то числа стануть рівними. Знайдіть початкові значення чисел.
Достатній рівень
1. Розв'яжіть рівняння: 0,7 · (6 у - 5) = 0,4 · (у - 3) - 1,16.
2. Катер плив 4 год за течією річки і 6 год проти течії річки. Шлях, який проплив катер за течією річки, на 9 км більший від шляху, який проплив катер проти течії. Знайдіть власну швидкість катера, якщо швидкість течії річки дорівнює 2,5 км/год.
Високий рівень
1. Розв'яжіть рівняння: 
.
2. Шнурок розрізали на дві частини так, що однієї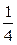 
частини дорівнює 
іншої частини. Знайдіть довжину кожної частини, якщо різниця їх довжин дорівнює 50 см.
3. За яких значень а рівняння (2 а + 1) х = -6 а + 2 х - 13 має корінь, який дорівнює -1?
4. Знайдіть добуток коренів рівняння 12: | х | - 6,06 = -0,06.
5. З пункту А до пункту В виїхав велосипедист. Через 0,6 год услід за ним виїхав мотоцикліст, швидкість якого на 20 км/год більша від швидкості велосипедиста. Через 2,4 год після відправлення мотоцикліст проїхав на 36 км більше від велосипедиста. Знайдіть швидкість велосипедиста.
