Тема. Розв’язування задач за допомогою рівнянь
Мета. Продовжити формувати навички розв'язування задач з елементами письмового пояснення.
Тип уроку. Урок формування умінь і навичок.
Хід уроку
I. 
Перевірка домашнього завдання.
Задача 1280
Нехай одне число – х, а інше - 3х, а їх різниця3х-х, що за умовою маємо132
Отримаємо рівняння
3х-х=132,
2х=132,
х=132:2,
х=66.
отже перше число 66, а інше 198
Відповідь: 66 і 198 дані числа.
Подумай уважно і знайди відповідь.
Яке з рівнянь відповідає умові задачі: «У першій шафі було у 4 рази менше книжок, ніж у другій. Коли в першу шафу поклали 17 книжок, а з другої взяли 25, то в обох шафах книжок стало порівну. Скільки книжок було в кожній шафі спочатку?»
(За х позначимо початкову кількість книжок у першій шафі.)
а)х+25 = 4х-17; б) х+17 = 4х-25; в) х+17 = х-25; г) 4х+17 = х-25
Відгадай загадку.
Загадкове, нам знайоме,
В ньому є щось невідоме.
Його треба розв’язати,
Тобто корінь відшукати.
Кожен легко, без вагання
Відповість, що це - …
Пригоди Поспішайка
Кажуть: «Поспішиш — людей насмішиш». Так трапилося і цього разу. Учитель дав завдання розв'язати рівняння: 2 х - 4 = 5 х - 10.
Поспішайко пригадав розподільний закон множення і миттю перетворив це рівняння так: 2 · (х - 2) = 5 · (х - 2).
Потім поділив обидві його частини на х - 2 і вийшло 2 = 5(!) З того, що 2 ≠ 5, Поспішайко зробив висновок, що задане рівняння не має розв'язку.
Чи правильно це?
Подумай над цим завданням, як би ти розв’язав це рівняння? Пригадай!!!
7. Що називається рівнянням?
8. Що називається розв’язком, або коренем рівняння?
II. Формування умінь і навичок.
Розв'язування задач і вправ.
Проглянь зразки розв’язання задачі запиши їх в зошит.
№ 1283.
Умова
У двох цистернах зберігається 64т бензину, до того ж, маса бензину в першій цистерні становить 
маси в другій. Скільки бензину в кожній цистерні?
Нехай у другій цистерні є х т бензину, тоді в першій буде 
х т. Разом у двох цистернах є 
т, що за умовою задачі становить 64 т. Одержали рівняння: х + х = 64. Розв'яжемо його:
1 х = 64;
х = 64: 1 ; 
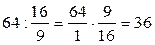
х = 36.
Отже, у другій цистерні є 36 т бензину, а в першій — 36 · =28 (т).
Відповідь. 28 т, 36 т.
№ 1285.
Умова
Турист 3 год їхав на велосипеді і 2 год йшов пішки, до того ж, пішки він пройшов на 6 
повільніше, ніж їхав на велосипеді. З якою швидкістю ішов турист, якщо всього він подолав 38км?
Нехай швидкість туриста на велосипеді дорівнює х км/год, тоді швидкість туриста пішки — (х - 6) км/год. Велосипедом він проїхав 3 х км, а пішки прой- шов 2(х - 6) км. Разом турист подолав 3 х + 2(х - 6) (км), що за умовою задачі дорівнює 38 км. Одержимо рівняння: 3 х + 2(х - 6) = 38. Розв'яжемо його:
3 х + 2 х - 12 = 38;
5 х = 38 + 12;
5 х = 50;
х = 10.
Отже, швидкість туриста на велосипеді дорівнює 10 км/год,
а пішки — 10 – 6 = 4 (км/год).
Відповідь. 4 км/год.
№ 1286.
Умова
Автомобіль проїхав деякий шлях за 2,5год. Якби він їхав швидше на 15 км/год, то проїхав би цей шлях за 2год. З якою швидкістю їхав автомобіль і який шлях він проїхав?
Нехай початкова швидкість автомобіля дорівнює х км/год, тоді за 2,5 год він проїхав шлях 2,5 х Якщо швидкість становитиме (х+ 15) км/год, то він проїде за 2 год шлях 2(х+ 15). За умовою, ці шляхи рівні. Одержимо рівняння: 2,5 х = 2 · (х + 15). Розв'яжемо його:
2,5 х = 2 х + 30;
2,5 х - 2 х = 30;
0,5 х = 30;
х = 60.
Отже, автомобіль їхав зі швидкістю 60 км/год і проїхав шлях 60 · 2,5 = 150 (км).
Відповідь. 60 км/год; 150 км.
№ 1288.
Умова
Магазин продав за 3 дні 460кг овочів. За перший день було продано овочів на 20кг менше, а за третій – в 1,2 разу більше, ніж за другий. Скільки овочів продав магазин за кожен день?
Нехай за другий день продали х кг овочів, тоді за перший день продали (х - 20) кг, а за третій — 1,2 х кг овочів. За три дні продали х + х - 20 + 1,2 х, що за умовою становить 460 кг овочів. Одержимо рівняння: х + х - 20 + 1,2 х = 460. Розв'яжемо його:
3,2 х - 20 = 460;
3,2 х = 460 + 20;
3,2 х = 480;
х = 150.
Отже, другого дня продали 150 кг, першого — 150 - 20 = 130 (кг), а третього — 1,2 · 150 = 180 (кг) овочів.
Відповідь. 130 кг; 150 кг; 180 кг.
№ 1290.
Умова
Периметр трикутника дорівнює 32см. Перша сторона вдвічі довша від другої, а друга – на 4 см коротша від третьої. Знайдіть довжину кожної сторони трикутника.
Нехай друга сторона трикутника дорівнює х см, тоді перша дорівнюватиме 2 х см, а третя — (х + 4) см. Периметр трикутника дорівнює х + 2 х + х + 4, що за умовою задачі становить 32 см. Одержимо рівняння: х + 2 х + х + 4 = 32. Розв'яжемо його:
х + 2 х + х + 4 = 32;
4 х = 32 - 4;
4 x = 28;
x = 7
Отже, друга сторона трикутника дорівнює 7 см, перша — 7 · 2 = 14 (см), а третя — 7 + 4 = 11 (см).
Відповідь. 14 см; 7 см; 11 см.
Розв’яжіть задачі самостійно і зробіть відповідні записи в зошиті.
Перевір себе:
Відповідь: 65т, 50т.
Якщо ти отримав такий результат, ти молодець! Правильно розв’язав задачу.
ІІІ. Пояснення домашнього завдання
№№ 1284, 1287.
Умова
№1284.Два трактори зорали 64га поля, до того ж, перший трактор зорав 0,8 того, що зорав другий. Скільки землі зорав кожний трактор?
№1287. Перший поїзд долає шлях між двома містами за 2,5год, а другий – за 3,5 год. Швидкість першого поїзда більша від швидкості другого поїзда на 24км/год. Знайдіть швидкість кожного поїзда і відстань між містами.
1. У вправі 1284 подумай, роботу якого трактора ти приймеш за х, потім звернись до завдання 1283 і подумай яку частину поля зорав другий трактор.
Я сподіваюсь, що ти знайдеш правильну відповідь.
