Метод Ньютона застосовується до розв’язування задачі (1), де f (x) є неперервно-диференційованою функцією. На початку обчислень вибирається початкове наближення x 0. Наступні наближення обчислюються за формулою
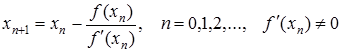. (23)
З геометричної точки зору xn+ 1 є значенням абсциси точки перетину дотичної до кривої y=f (x) в точці (xn, f (xn)) з віссю абсцис. Тому метод Ньютона називають також методом дотичних.
Теорема 2. Якщо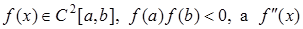 
не змінює знака на [a,b], то виходячи з початкового наближення 
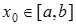, що задовольняє умові 
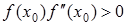, можна обчислити методом Ньютона єдиний корінь 
рівняння (1) з будь-якою степінню точності.
Теорема 3. Нехай - простий дійсний корінь рівняння (1) і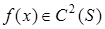 
, де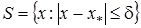 
,
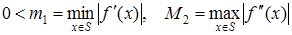, (24)
причому
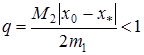. (25)
Тоді для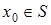 
метод Ньютона збігається, причому для похибки справедлива оцінка
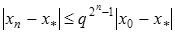. (26)
З оцінки (26) видно, що метод Ньютона має квадратичну збіжність, тобто похибка на (n+ 1) - й ітерації пропорційна квадрату похибки на n- й ітерації.
Модифікований метод Ньютона
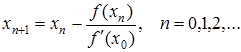(27)
дозволяє не обчислювати похідну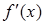 
на кожній ітерації, а отже і позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність.
Кількість ітерацій, які потрібно провести для знаходження розв’язку задачі (1) з точністю e задовольняє нерівності
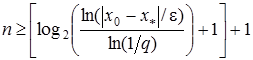. (28)
Приклад 1. Розв’язати рівняння
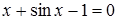(29)
методом ділення проміжку навпіл з точністю e=10-4.
Розв’язання. Спочатку знайдемо проміжок, де рівняння має єдиний корінь. Оскільки похідна функції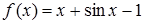 
не змінює знак, то корінь у рівнянні (29) буде один. Легко бачити, що f (0) = -1 < 0, а 
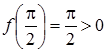. Отже корінь належить проміжку 
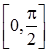. Виберемо 
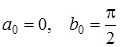. Згідно з формулою (6), отримаємо, що для знаходження кореня з точністю 10-4 необхідно провести 13 інтеграцій. Відповідні значення xn наведені в табл. 1.
Табл.1
| n | xn | f (xn) |
| 0785398E+00 | 0492505E+00 | |
| 0392699E+00 | 0224617E+00 | |
| 0589049E+00 | 0144619E+00 | |
| 0490874E+00 | 0377294E-01 | |
| 0539961E+00 | 0540639E-01 | |
| 0515418E+00 | 0831580E-02 | |
| 0503146E+00 | 0146705E-01 | |
| 0509282E+00 | 0316819E-02 | |
| 0512350E+00 | 0257611E-02 | |
| 0510816E+00 | 0295467E-03 | |
| 0511583E+00 | 0114046E-02 | |
| 0511199E+00 | 0422535E-03 | |
| 0511007E+00 | 0635430E-04 | |
| 0510911E+00 | 0116016E-03 |
Приклад 2. Знайти додатні корені рівняння
x 3- x -1 = 0 (30)
методом простої ітерації з точністю e=10-4.
Розв’язання. Графічне дослідження рівняння (30) показує, що існує єдиний дійсний додатній корінь цього рівняння і він належить проміжку [1,2]. Оскільки на цьому проміжку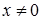 
, то рівняння (30) можна подати у вигляді
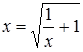. (31)
Позначимо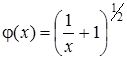 
. Перевіримо виконання умов теореми про збіжність методу простої ітерації. Виберемо x 0 = 1,5, тоді d = 0,5. Розглянемо
,
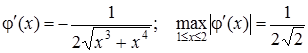тобто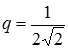 
.
тоді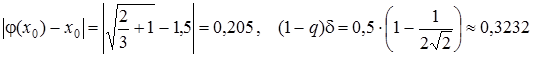 
,
а отже умова (12) виконується. З формули (15) маємо, що кількість ітерацій, які необхідно провести для знаходження кореня з точністю e=10-4 повинна задовольняти умові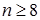 
. Відповідні значення xn та xn -j(xn) наведені в табл.2.
Табл.2
| n | xn | xn -j(xn) |
| 0150000E+01 | 0209006E+00 | |
| 0129099E+01 | 0411454E-01 | |
| 0133214E+01 | 0901020E-02 | |
| 0132313E+01 | 0193024E-02 | |
| 0132506E+01 | 0415444E-03 | |
| 0132464E+01 | 0892878E-04 | |
| 0132473E+01 | 0191927E-04 | |
| 0132471E+01 | 0417233E-05 | |
| 0132472E+01 | 0953674E-06 |
Виходячи з нерівності (16) і отриманих результатів видно, що для досягнення заданої точності достатньо було провести 5 ітерацій (n= 5). Взагалі слід відзначити, що апостеріорна оцінка (16) є більш точною і її використання може заощадити деяку кількість обчислень.
Приклад 3. Методом релаксації знайти найменший за модулем від’ємний корінь рівняння
x 3-3 x 2-1 = 0 (32)
з точністю e=10-4.
Розв’язання. Спочатку виділимо корені рівняння (32) користуючись наступною таблицею
Табл.3
| x | -4 | -3 | -2 | -1 | ||||
| sign f (x) | - | - | + | + | - | + | + | + |
З даної таблиці видно, що рівняння має три корені розташовані на проміжках [-3;-2], [-1;0], [0;1]. Будемо знаходити корінь на проміжку [-1;0]. Обчисливши значення f (-0,5) = -0,375 можна уточнити проміжок існування кореня [-1;-0,5].
Позначимо f (x) =x 3-3 x 2-1. Тоді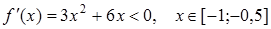 
і є монотонно зростаючою функцією на [-1;-0,5] (оскільки 
).
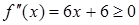Тому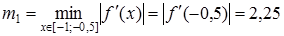 
,
.
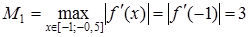Тоді, відповідно до формул (20) і (21), будемо мати вигляд
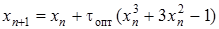. (33)
Вибравши за початкове наближення точку x 0 = -0,5 будемо мати оцінку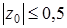 
, а кількість ітерацій, які потрібно провести для знаходження розв’язку з точністю e=10-4 буде дорівнювати 5 (див. (22)). В табл. 4 наведені відповідні дані ітераційної послідовності:
Табл.4
| n | xn | f (xn) |
| 0500000E+00 | 0142857E+00 | |
| 0642857E+00 | 0985700E-02 | |
| 0652714E+00 | 0105500E-04 | |
| 0652704E+00 | 0596046E-07 | |
| 0652704E+00 | 0000000E+00 | |
| 0652704E+00 | 0000000E+00 |
Із наведених даних видно, що необхідна точність досягається раніше 5-ї ітерації. Це досить характерно для апріорних оцінок типу (22).
Приклад 4. Методом Ньютона знайти найменший додатній корінь рівняння
x 3+3 x 2-1 = 0 (34)
з точністю e=10-4.
Розв’язання. З табл. 3 видно, що рівняння (34) має єдиний додатній корінь, що належить проміжку [0;1]. обчислимо f (0,5) = -0,125. Тепер будемо шукати корінь на проміжку [0,5;1]. Нехай f (x) =x 3+3 x 2-1. Тоді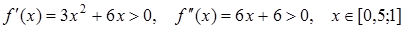 
.
,
.
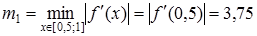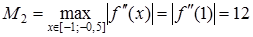Виберемо x 0 = 1, тоді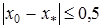 
. З формули (25) маємо
.
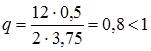Тобто всі умови теореми про збіжність методу Ньютона виконані. З формули (28) маємо, що для досягнення заданої точності достатньо провести 7 ітерацій. Відповідні обчислення наведені в табл. 5.
Табл.5
| n | xn | f (xn) |
| 01000000E+01 | 03000000E+01 | |
| 06666667E+00 | 06296297E+00 | |
| 05486111E+00 | 06804019E-01 | |
| 05323902E+00 | 01218202E-02 | |
| 05320890E+00 | 04395228E-06 | |
| 05320889E+00 | 04230802E-07 | |
| 05320889E+00 | 04230802E-07 | |
| 05320889E+00 | 04230802E-07 |
Задачі
Знайти одним з ітераційних методів дійсні корені рівнянь з точністю e (наприклад e=10-4 ).
1) 
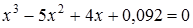
2) 
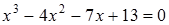
3) 
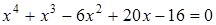
4) 
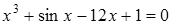
5) 
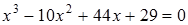
6) 
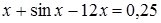
7) 
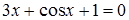
8) 
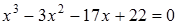
9) 
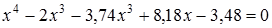
10) 
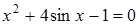
11) 
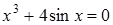
12) 
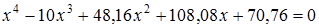
13) 
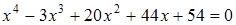
14) 
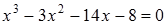
15) 
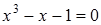
16) 
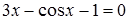
17) 
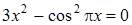
18) 
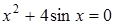
19) 
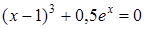
20) 
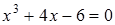
21) 
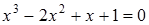
22) 
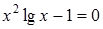
23) 
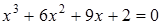
24) 
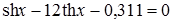
25) 
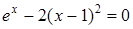
26) 
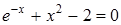
27) 
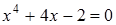
28) 
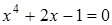
29) 
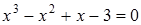
30) 
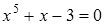
31) 
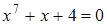
32) 
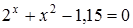
33) 
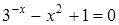
34) 
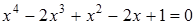
35) 
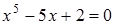
36) 
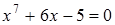
37) 
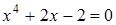
38) 
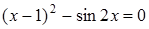
39) 
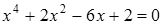
40) 
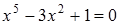
41) 
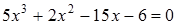
42) 
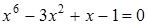
43) 
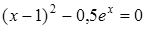
44) 
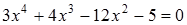
45) 
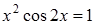
46) 
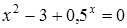
47) 
