Метод простої ітерації застосовується до розв’язування нелінійного рівняння виду
. (7)
Перейти від рівняння (1) до рівняння(7) можна багатьма способами, наприклад, вибравши
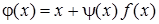, (8)
де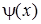 
- довільна знакостала неперервна функція.
Вибравши нульове наближення x 0, наступні наближення знаходяться за формулою
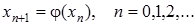. (9)
Наведемо достатні умови збіжності методу простої ітерації.
Теорема 1. Нехай для вибраного початкового наближення x 0 на проміжку
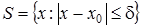(10)
функція j(x) задовольняє умові Ліпшиця
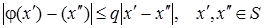(11)
де 0 <q< 1, і виконується нерівність
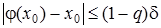. (12)
Тоді рівняння (7) має на проміжку S єдиний корінь 
, до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю
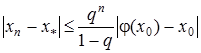. (13)
Зауваження: якщо функція j(x) має на проміжку S неперервну похідну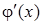 
, яка задовольняє умові
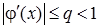, (14)
то функція j(x) буде задовольняти умові (11) теореми 1.
З (13) можна отримати оцінку кількості ітерацій. які потрібно провести для знаходження розв’язку задачі (7) з наперед заданою точністю e:
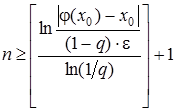. (15)
Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:
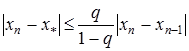. (16)
