Постановка задачі:
Розглянемо задачу знаходження коренів рівняння
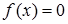 , (1)
, (1)
де  - задана функція дійсного змінного.
- задана функція дійсного змінного.
Розв’язування даної задачі можна розкласти на декілька етапів:
а) досліджена розташування коренів (в загальному випадку на комплексній площині) та їх кратність;
б) відділення коренів, тобто виділення областей, що містять тільки один корінь;
в) обчислення кореня з заданою точністю за допомогою одного з ітераційних алгоритмів.
Далі розглядаються ітераційні процеси, що дають можливість побудувати числову послідовність xn, яка збігається до шуканого кореня  рівняння (1).
рівняння (1).
1. Метод ділення проміжку навпіл (метод дихотомії)
Нехай  і відомо, що рівняння (1) має єдиний корінь
і відомо, що рівняння (1) має єдиний корінь 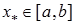 . Покладемо a 0 =a, b 0 =b, x 0 = (a 0 +b 0)/2. Якщо
. Покладемо a 0 =a, b 0 =b, x 0 = (a 0 +b 0)/2. Якщо 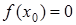 , то
, то  . Якщо
. Якщо 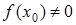 , то покладемо
, то покладемо
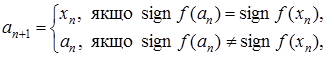 (2)
(2)
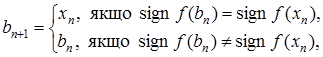 (3)
(3)
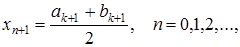 (4)
(4)
і обчислимо 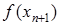 . Якщо
. Якщо 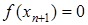 , то ітераційний процес зупинимо і будемо вважати, що
, то ітераційний процес зупинимо і будемо вважати, що 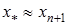 . Якщо
. Якщо  , то повторюємо розрахунки за формулами (2)-(4).
, то повторюємо розрахунки за формулами (2)-(4).
З формул (2), (3) видно, що  і
і  . Тому
. Тому  , а отже шуканий корінь
, а отже шуканий корінь  знаходиться на проміжку
знаходиться на проміжку 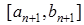 . При цьому має місце оцінка збіжності
. При цьому має місце оцінка збіжності
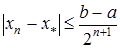 . (5)
. (5)
Звідси випливає, що кількість ітерацій. які необхідно провести для знаходження наближеного кореня рівняння (1) з заданою точністю e задовольняє співвідношенню
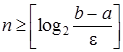 . (6)
. (6)
де [ c ] - ціла частина числа c.
Серед переваг даного методу слід відзначити простоту реалізації та надійність. Послідовність { xn } збігається до кореня  для довільних неперервних функцій f (x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
для довільних неперервних функцій f (x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.






