4a2x2+ 4abx+ 4ac=0;
(2ax+b)2-(b2-4ac)=0;
(2ax+b)2-( )2=0.
)2=0.
На перших етапах формування вмінь та навичок розв’язівати квадратні рівняння доцільно виконуючи записи.
Наприклад.
2х2-х-3=0;
а=2; b=1; c=-3;
D=(-1)2-4  2(-3)=25;
2(-3)=25;
x1=  =
=  =
=  ;
;
x2= 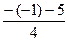 =-
=-  =-1.
=-1.
Звертається увага на дослідження коренів квадратного рівняння:
1) D  0;
0;
2) D=0;
3) D  0.
0.
Дослідити квадратне рівняння ax2+bx+c=0 означає не розв’язати його, а встановити:
1. якій числовій множині належать його корені;
2. якщо корені дійсні, вияснити їх кількість та знаки;
3. якщо знаки різні, визначити, який корінь має більшу абсолютну величину. 
| D | a | b | c | x1 | x2 | Примітка |
| + | + | - | + | + | + | |
| + | + | + | + | - | - | |
| + | + | + | - | - | + |   
|
| + | + | - | - | - | + |   
|
| + | - | + | + | + | x1=x2 | |
| + | + | + | - | - | x1=x2 | |
| - | + | + | + | Дійснич коренів не має. | ||
| - | + | - | + |
x2+ 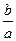 x+
x+  =0
=0
1. Якщо 
 0, то х1х2
0, то х1х2  0, х1 і х2 одного знаку:
0, х1 і х2 одного знаку:
а) - 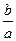
 0, х1 + х2
0, х1 + х2  0
0  х1
х1  0 і х2
0 і х2  0;
0;
б) - 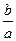
 0, х1 + х2
0, х1 + х2  0
0  х1
х1  0 і х2
0 і х2  0;
0;
2. Якщо 
 0, то х1х
0, то х1х  0, х1 і х2 - різні знаки:
0, х1 і х2 - різні знаки:
а) - 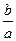
 0, х1 + х2
0, х1 + х2  0,
0, 

 ;
;
б) - 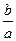
 0, х1 + х2
0, х1 + х2  0
0 


 ;
;
3. Якщо b=0, 
 0, то
0, то  =
=  .
.
Для квадратних рівнянь мають місце такі твердження:
1. Якщо у даному квадратному рівнянні поміняти коефіцієнт а і с, то одержимо рівняння, корені якого обернені даним
ax2+bx+c=0; x1: x2
cx2+bx+a=0;  і
і 
c  +
+  +a=c
+a=c  ax2+bx+c=0.
ax2+bx+c=0.
2. Якщо у квадратному рівнянні ax2+bx+c=0 поміняти знак біля коефіцієнту b, то одержимо рівняння, корені якого протилежні кореням даного;
3. Якщо у квадратному рівнянні а і с мають різні знаки, то рівняння має дійсні корені;
4. Якщо а  0 і D=0, то ліва частина квадратного рівняння є повний квадрат;
0 і D=0, то ліва частина квадратного рівняння є повний квадрат;
5. Якщо a+b+c=0, то х1=1, х2=  ;
;
6. Якщо a-b+c=0, то х1=-1, х2=-  .
.
Важливим моментом при вивченні квадратних рівнянь є розгляд теореми Вієта (пряма і обернена). Складність засвоєння теореми Вієта зв’язана з декількома обставинами. Слід розуміти різницю між прямою і оберненою теоремами. Школярі часто роблять помилку посилаючись на ту, чи іншу теорему Вієта. Наприклад, при знаходженні коренів квадратного рівняння підбором, треба користуватись оберненою теоремою, а не прямою, як часто роблять.
Після вивчення теореми Вієта обов’язково розв’язуються задачі такого змісту:
1. знаходження знаків кількох рівняння;
2. знаходження знаків коренів рівняння;
3. складання квадратного рівняння за даними коренями;
4. знаходження коефіцієнта квадратного рівняння за відповідними даними.
Деякі прийоми усного розв’язування квадратних рівнянь з раціональним коренем:
1) ax2+bx+c:
а) відкинення коефіцієнта а;
б) помножити вільний член на а;
в) взяти два числа, добуток яких дорівнює ас, а сума дорівнює b;
г) кожне із знайдених чисел поділити на а;
2) x2+px+q, q=m2h, p=md:
а) знаходження множників m і m2, на які діляться p і q на m і m2;
б) знаходяться частки к і l від дільників p іq на m і m2;
в) шукають два числа, добуток яких дорівнює l, а сума к з протилежним знаком;
г) знаходження числа множеного на m.
 Теорема Вієта (пряма). Якщо квадратне рівняння має дійсні корені, то х1+х2=-
Теорема Вієта (пряма). Якщо квадратне рівняння має дійсні корені, то х1+х2=- 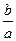
х1х2=  .
.
Теорема Вієта (обернена). Якщо числа m і n такі, що їх сума дорівнює –р, а добуток дорівнює q, то ці числа є коренями квадратного рівняння x2+px+q=0.
 Доведення. m+n=-p
Доведення. m+n=-p
mn=q;
x2-(m+n)x+mn=0;
x2-mx=nx+mx=0  x(x-m)n(x-m)=0
x(x-m)n(x-m)=0  (x-m)(x-n)=0.
(x-m)(x-n)=0.
Нехай х1,х2 – корені рівняння x2+px+q і Sn=x1n+x2n, (n  2, n’N), тоді правильна рекурентна формула
2, n’N), тоді правильна рекурентна формула
Sn+1=-pSn-qSn-1, S1=-p, S2=p2-2q.
Доведення. х1,х2 – корені рівняння, тому
 х12+px1+q=0/
х12+px1+q=0/  х1n-1;
х1n-1;
х22+px2+q=0/  х2n-1;
х2n-1;
 x1n+1+px1n+qx1n-1=0
x1n+1+px1n+qx1n-1=0
x2n+1+px2n+qx2n-1=0;
x1n+1+x2n+1+p(x1n+x2n)+q(x1n-1+x2n-1)=0.
Теорему доведено.
Приклад.
2х2-5х+1
х1+х2= 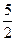 ;
;
х1х2=  ;
;
х13+х23= 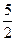 (
( -
-  )=
)=  .
.






