Лекція
Методика вивчення рівнянь у основній школі
Вступ
Рівняння і системи рівнянь пронизують весь курс шкільної математики. Найпростіші рівняння учні розв’язують ще у початковій школі. Але букву х називають не змінною, а невідомим числом.
Всі класи рівнянь та їх систем можна поділити на дві групи.
Перша група – раціональні рівняння та їх системи. Найбільш важливими класами у цій групі є:
1) лінійні рівняння з однією змінною;
2) лінійні рівняння з двома змінними;
3) системи лінійних рівнянь з двома змінними;
4) квадратні рівняння;
5) лінійні нерівності з однією змінною;
6) квадратні нерівності.
Друга група – ірраціональні, показникові, логарифмічні, тригонометричні рівняння.
Перша група вивчається у 7-9 класах, а друга в 10-11 класах.
Послідовність вивчення різних класів рівнянь та їх систем різна у різних підручниках. Однак, кількість можливих варіантів для послідовності їх введення невелика, бо класи рівнянь перебувають у певній логічній залежності, яка впливає на порядок їх появи у шкільному курсі.
Спочатку вивчають рівняння, а потім їх системи. Таке роздільне вивчення проводиться до теорії квадратного тричлена, яка вивчається у 9-му класі.
1. Пропедевтика вивчення систематичного курсу рівнянь
Найпростіші рівняння та їх системи учні розв’язують ще у початковій школі.
У 5-му класі розкривається зміст таких понять, як рівняння (рівність, що містить невідоме число називається рівнянням; значення невідомого, при якому рівняння перетворюється у правильну числову рівність, називається розв’язком або коренем рівняння).
Розв’язати рівняння, означає знайти всі його корені. Рівняння розв’язується на основі залежностей між компонентами чотирьох арифметичних дій.
У 6-му класі учні розв’язують рівняння, яке містить змінну, як у лівій, так і правій частинах. Після вивчення розподільного закону множення значно розширюється круг задач, що розв’язуються за допомогою рівнянь.
В міру вивчення теоретичного матеріалу вводять нові види рівнянь та їх систем. Крім цього розширюється множина розв’язків рівнянь та їх систем, бо вивчаються від’ємні раціональні числа, розв’язуються найпростіші рівняння з модулями, рівняння, що містять дужки, вводиться поняття коефіцієнту та застосовуються поступово нові способи розв’язування рівнянь (за допомогою додавання до обох частин рівняння x+a=b числа, протилежного до а, перенесення доданків з однієї частини в другу, зведення подібних доданків, ділення обох частин на коефіцієнт при невідомому).
Наприклад:
2(х+3)=3(х-4);
2х+6=3х-12;
2х-3х=-12-6;
-х=-18;
х=18.
Коли учні зрозуміли що таке рівняння, можна вводити поняття розв’язку рівняння. Один з методичних прийомів є застосування таблиць:
 х х
| 
| -2 | ||
| 5х+4=3х | 5+4=3 | 0+4=0 | 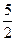 +4= +4= 
| -10+4=-6 |
| Правильно | ------- | ------- | ------- | прав. |
| Неправильно | непр. | непр. | непр. | ------ |
Таблиці заповнюються у процесі евристичної бесіди.
Систематичне вивчення теорії про рівняння розпочинається у курсі алгебри 7-го класу.
У цілому розгляд теоретичного матеріалу про рівняння у 7-9 класах проводиться переважно на індуктивному рівні з використанням елементів дедукції.
Загальне поняття рівняння та його властивості вводяться індуктивно, але розгляд окремих видів рівнянь проводиться з використанням елементів дедуктивних міркувань.
Наприклад, поняття лінійного рівняння з однією змінною вводиться за означенням, у якому відправним пунктом є загальний вигляд лінійного рівняння.
В усіх класах формування поняття рівняння і вироблення навичок їх розв’язування проводиться на простих вправах, з метою, щоб технічне розв’язання не закривала суті питання.
У 8-му класі вивчаються квадратні рівняння, розв’язуються раціональні рівняння, дробово-раціональні рівняння, графічний спосіб розв’язування квадратних рівнянь.
У 9-му класі вивчаються рівняння і системи рівнянь, графічний розв’язок системи рівнянь, рівняння 3-го і 4-го степеня з однією змінною, які розв’язуються за допомогою розкладання на множники і введення допоміжної змінної. Вводиться поняття рівносильності рівнянь (якщо корені 1-го рівняння є корені 2-го, а корені 2-го є корені 1-го, то ці рівняння рівносильні).
Наприклад:
2х+3=8 2х+3+10=8+10
х=2,5, х=2,5.
Загальні теоретичні положення про рівняння
Систематичне вивчення теорії рівнянь розпочинається з 7-го класу.
Основна мета – систематизувати і узагальнити відомості про розв’язання рівнянь з однією змінною. Розширити поняття про рівняння, їх види та методи розв’язання.
У 7-му класі дається означення рівняння, вводяться основні поняття. Загальне поняття рівняння і його властивості вводяться індуктивно, а розгляд окремих видів рівнянь здійснюється з використанням елементів дедуктивних міркувань.
| Клас | Зміст матеріалу | Основні поняття |
| Загальні відомості про рівняння. Властивості рівнянь | Рівняння, корінь (розв’язок) рівняння, розв’язати рівняння, ліва, права частини рівняння, рівносильність рівнянь. | |
| Лінійні рівняння з однією змінною ax=b. Лінійні рівняння з двома змінними ax+by=c. Системи лінійних рівнянь з двома змінними. | Графік лінійного рівняння,пара чисел розв’язку рівняння системи рівняння. | |
| Квадратні рівняння. Дробово-раціональні рівняння. | ||
| Біквадратне рівняння. Нелінійні системи рівнянь. |
Означення 1. Рівняння f(x)=  (х) називається алгебраїчним, якщо f(x) і
(х) називається алгебраїчним, якщо f(x) і  (х) – многочлени. Рівняння називається дробово-раціональним, якщо f(x) і
(х) – многочлени. Рівняння називається дробово-раціональним, якщо f(x) і  (х) – раціональні функції, причому хоча б одна з них дробово-раціональна відносно змінної х.
(х) – раціональні функції, причому хоча б одна з них дробово-раціональна відносно змінної х.
Означення 2. Рівняння називається ірраціональним, якщо f(x) і  (х) – елементи алгебраїчної функції і хоча б одна з них ірраціональна відносно змінної х.
(х) – елементи алгебраїчної функції і хоча б одна з них ірраціональна відносно змінної х.
Означення 3. Рівняння називається трансцендентним, якщо (x) і  (х) – елементи функції і хоча б одна з них трансцендентна відносно змінної х.
(х) – елементи функції і хоча б одна з них трансцендентна відносно змінної х.
Класифікація рівнянь
 |
Розв’язати рівняння можна на різних теоретичних основах.
Є такі способи розв’язання рівнянь в основній школі:
1) на основі залежностей між компонентами та результатами дій;
2) за властивостями рівностей;
3) за теоремами про рівносильність рівнянь;
4) графічний спосіб.
У 8-му класі вивчаються рівняння із змінною у знаменнику. Розв’язувати їх можна двома способами:
1) зведення рівняння до виду 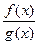 =0, яке зводиться до системи
=0, яке зводиться до системи
 f(x)=0
f(x)=0
g(x) 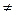 0;
0;
2) зведення до виду 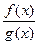 =
= 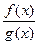 , яке зводиться до системи
, яке зводиться до системи
 f(x)=f1(x)
f(x)=f1(x)
g(x) 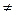 0.
0.
Означення 1. Рівняння Pn(x)=0, де Pn(x) – ціла раціональна функція n-го степеня, називається алгебраїчно раціональним рівнянням n-го степеня.
Наприклад. 2х+7=0, 3х2-5х+8=0, 5х3-4х2+2=0.
Раціональні рівняння поділяються на:
1. Лінійні рівняння – рівняння виду ax+b=0, де a і b – деякі числа, причому а 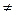 0. Його ще називають рівнянням першого степеня (бо має єдиний розв’язок х=-
0. Його ще називають рівнянням першого степеня (бо має єдиний розв’язок х=- 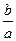 ). Якщо не має умови а
). Якщо не має умови а 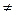 0, називається лінійним рівнянням, яке має більше розв’язків:
0, називається лінійним рівнянням, яке має більше розв’язків:
а) а 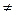 0, ax+b=0
0, ax+b=0  х=-
х=- 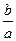 ;
;
б) а=0, b=0, ax+b=0  хєR;
хєR;
в) а=0, b 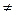 0, ax+b=0
0, ax+b=0  хє
хє 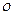 .
.
2. Квадратні рівняння – це рівняння виду ax2+bx+c=0, де a,b,c – деякі числа, причому а 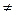 0.
0.
Розрізняють повні та неповні квадратні рівняння.






