Виконавши у рівняння ах-3 = b тотожні перетворення, дістанемо: ах = b+3.
1) якщо а≠0, то х = 
при будь – якому b;
2) якщо а =0, то при b= -3 рівняння набуває вигляду 0х=0, тобто коренями рівняння є всі числа;
3) якщо а=0 і b≠-3, дістанемо 0х = b +3 ≠0, така рівність неможлива, тому рівняння коренів не має.
Відповідь. при а ≠0 і будь – якому b х = ; при а =0 і b = -3 корені рівняння – всі числа; при а=0 і b≠0 коренів немає.
Приклад 2. Розв’язати рівняння:
(а-1)(а+1)х – а -1 =0 залежно від а.
Розв’язання.
Запишемо рівняння у вигляді: (а-1)(а+1)х = а+1.
Добуток (а-1)(а+1) дорівнює нулю при а =1 або
а = -1, тому розглянемо такі випадки:
1)при а = 1 рівняння набуває вигляду 0х = 2, яке коренів не має;
2)при а = -1 дістанемо рівняння 0х =0, корені якого є всі числа;
3)при | а| ≠1 (а-1)(а+1) ≠0, тому 
х =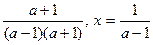 
.
Відповідь: при |а| ≠1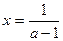 
; при а = -1 корені рівняння – всі числа; при а = 1 – коренів не має.
Приклад 3.Розв’язати рівняння:
(а+4)х – 2,5х = (а-2)(а+3) + 3,5х.
Розв’язання.
Перетворимо дане рівняння, скориставшись основними властивостями рівнянь:
(а+4)х – 2,5х -3,5х = (а-2)(а+3),
(а+4-2,5 -3,5)х = (а-2)(а+3), (а-2)х = (а-2)(а+3).
Якщо а ≠2, то рівняння має єдиний корінь
.
Якщо а = 2, то рівняння набуває вигляду 0х =0, його коренями є всі числа.
Відповідь: при а≠2 х = а+3; при а =2 корені всі числа.
Приклад 4. Розв’язати рівняння:
7,5 х – 2ах –а2= 5,5х – 3ах -4.
Розв’язання.
Скориставшись властивостями рівнянь, виконаємо в ньому перетворення:
7,5х – 2ах – 5,5х +3ах = а2-4,
(а+2)х = а2 -4, (а+2)х = (а-2)(а+2).
Якщо а = - 2, то рівняння набуває вигляду
0х =0 і його коренями є всі числа.
Якщо а ≠ -2, то рівняння має єдиний корінь
х= 
Відповідь: при а =-2 корені – всі числа; при а ≠2
х = а-2.
Приклад 5. Розв’язати рівняння:
|ах-1| = |х+3|.
Рівність | ах-1| = |х+3|. Виконується, якщо:
1) ах-1 = х+3;
2)ах-1 = - (х+3).
Розглянемо кожний випадок окремо.
1) ах -1 = х+3, ах -х = 4, (а-1)х =4.
Якщо а =1, то рівняння набуває вигляду 0х=4. Рівняння коренів не має.
Якщо а ≠1, то х=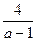 
.
2) ах -1 = - (х+3), ах-1 = -х-3, ах +х = -2, (а+1)х = -2.
Якщо а = -1, то рівняння набуває вигляду
0х = -2. рівняння коренів не має.
Якщо а ≠, то х= 
.
Відповідь: при |а| ≠1 х1= 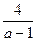, х2= ; при а = -1
х = 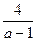; при а = 1 х = .
Приклад 6. Розв’язати рівняння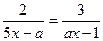 
.
Розв’язання. Маємо 2(ах-1) = 3(5х-а), звідки
(2а-15)х = 2-3а.
Якщо = 
то рівняння має вигляд 0х = -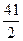 
. Це рівняння, а отже, і дане рівняння не мають розв’язків.
Якщо а ≠ то рівняння має єдиний корінь
х = 
Визначимо при яких значеннях а знайдений корінь задовольняє рівняння, тобто знайдемо область визначення.
Область допустимих значень невідомого і параметрів, що входять до рівняння, визначається рівняннями:
5х-а ≠0 та ах -1 ≠0. При х = дістанемо
Звідси
10-15а -2а2+15а ≠0 та 2а-3а2-2а+15 ≠0, а≠ 
Отже, якщо а ≠ та а≠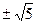 
, рівняння має єдиний корінь х =
Якщо а = рівняння не має коренів.
Приклад 7. Розв’язати рівняння 
Розв’язання. Область допустимих значень невідомого і параметрів х ≠0, х ≠ а.
Маємо а - х = bх, (b+1)х = а.
Якщо b = -1, а = 0, то рівняння а - х = bх, (b+1)х = а набирає вигляду 0х = 0. Це рівняння справджується для будь – яких значень х, що входять до області допустимих значень.
Якщо b = - 1, а ≠ 0, то рівняння набуває вигляду 0х = а. Коренів немає.
Якщо b ≠ - 1, то рівняння має єдиний розв’язок
х =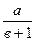 
.
Перевіримо, при яких значеннях параметрів а і b утворений корінь задовольняє рівняння.
Виходячи з умови, х ≠ 0 та а – х ≠0, Отже,
Звідси а ≠ 0 та b ≠ 0.
Отже, якщо b = -1, а =0, то рівняння має безліч коренів, тобто має смисл при будь – яких дійсних х, крім
х = 0, х =а.
Якщо b = – 1, а ≠0, то розв’язків немає.
Якщо х ≠ 0, а ≠ 0, b ≠ -1, то х = .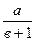
Приклад 8.Розв’язати рівняння 2m(m-2)х = m-2.
Тут контрольними будуть ті значення параметра, при яких коефіцієнт при х перетворюється в нуль, тобто m = 0 і m = 2. Отже, якщо m =0, m =2, то не можна ділити обидві частини рівняння на коефіцієнт при х, в той час як при значеннях параметра m ≠0, m ≠ 2 таке ділення можливе.
Звідси випливає, що доцільно розглянути рівняння 2m(m-2)х = m-2 для таких значень параметра:
1) m = 0; 2) m = 2; в) 
1) якщо m = 0, то рівняння 2m(m-2)х = m-2. набуде вигляду 0х = - 2. Це рівняння не має коренів.
2) якщо m = 2, то рівняння 2m(m-2)х = m- 2. набуде вигляду 0х = 0. Коренем цього рівняння буде будь – яке дійсне число.
3)якщо m ≠ 0 і m ≠ 2, то з рівняння 2m(m-2)х = m-2.
дістанемо х =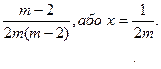 
Відповідь. Якщо m = 0, то коренів немає; якщо m =2, то коренем рівняння є будь – яке дійсне число; якщо то 
.
Приклад 9. Розв’язати рівняння 
відносно х.
Розв’язання.
ОДЗ: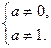 
після зведення дробів до спільного знаменника, перейдемо до лінійного рівняння відносно х.
ах + ах – х = 4а2 – 1, х(2а – 1) = 4а2 – 1.
Якщо а = 
, то рівняння набуває вигляду
0 
х = 0 і має безліч коренів.
При а ≠ х = 2а + 1.
Враховуючи ОДЗ параметра, запишемо відповідь.
Відповідь. При а = х – будь – яке число; при
а ≠ , а ≠ 0; а≠ 1 х = 2а + 1; при а = 0, а = 1 коренів немає.
Приклад 10. Розв’язати рівняння
(
2 – 1) 
= + 1.
Розв’язання. При розв’язуванні цього рівняння достатньо розглянути такі випадки:
1) = 1; тоді рівняння матиме вигляд 0 =2 і воно не має розв’язків;
2) = -1; отримуємо 0 = 0 і, очевидно, - будь – яке;
3) ≠ 
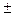1; маємо = 
.
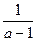Відповідь. Якщо = - 1, то - будь – яке число; якщо
= 1, то розв’язку немає; якщо ≠ 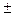1; маємо = .
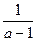Приклад 11. Розв’язати рівняння 
Розв’язання. В даному випадку = - єдиний корінь. Зрозуміло, що умова ≠ 1 вимагає виконання умови ≠ 1.
Відповідь. Якщо ≠1, то = ; якщо =1, то рівняння розв’язку немає.
Приклад 12.Розв’язати рівняння 
Розв’язання. Перейдемо до рівняння наслідку:
( + -1)( +1) – 3( +1) = 5 ;
2 + ( -3) - 4 -4 =0. звідси 1 =4, 2 = - -1. Для того, щоб знайдені значення були коренями вихідного рівняння, достатньо вимагати виконання умов: 1 ≠ 1 - , 2≠ -1,
1 ≠ -1, 2 ≠ 1 - . Виконання двох останніх умов очевидне.
Якщо 1 =1 - , тобто 4 = 1 - , то = -3. Тоді, якщо = -3,то значення 1 = 4 не є коренем даного рівняння. Тут важливо не зробити помилковий висновок, що при = - 3 взагалі коренів немає. Насправді для = -3 маємо 2 =2, і ніщо не заважає 2 =2 бути коренем вихідного рівняння.
Якщо 2 =-1, тобто - -1 = -1, то =0. Звідси якщо =0, то 2 – не корінь, а 1 – корінь даного рівняння.
Відповідь. Якщо = -3, то =2; якщо =0, то =4; якщо ≠0 і ≠ -3,
то =4 або = - -1.
Приклад 13. Розв’язати рівняння =1.
Розв’язання. На перший погляд, можна відразу дати відповідь: = 
Але якщо =0, то дане рівняння розв’язків не має.
Відповідь. Якщо =0, то рівняння розв’язків не має; якщо ≠ 0, то =
Приклад 14. Розв’язати рівняння| 2-1| + | ( -1) | = 0.
Розв’язання. Дане рівняння рівносильне системі
Маємо: 
Якщо ≠0, то друге рівняння системи і сама система мають єдиний розв’язок: =1.
Якщо ж =0, то з другого рівняння отримуємо, що - будь – яке. Отже, в цьому випадку система має два розв’язки: =1 або = -1.
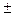Відповідь. Якщо ≠0, то =1; якщо =0, то = 1.
Приклад 15.Розв’язати рівняння
( -1) 
=0
Розв’язання. Дане рівняння рівносильне системі
Звідси = - корінь вихідного рівняння для будь – якого , а =1 – корінь лише, якщо ≤1
Відповідь. Якщо 
1, то = або =1; якщо =1, то =1; якщо 
1, то = .
Приклад 16. При яких рівняння 2- +3 =0 має єдиний розв’язок?
Розв’язування. Перш за все звернемо увагу на поширену помилку: вважати вихідне рівняння квадратним. Насправді це рівняння степеня не вище другого. У зв’язку із цим, природно почати розв’язання, розглянувши випадок, коли =0. Отже, якщо =0, то очевидно, що дане рівняння має єдиний розв’язок.
Якщо ж ≠0, то ми маємо справу із квадратним рівняння. Його дискримінант 1 - 12 набуває значень, що дорівнюють нулю, якщо = 
.
Відповідь. =0 або = .
Приклад 17.При яких значеннях рівняння ( -2) 2 +(4 - 2 ) +3 =0.
Розв’язування. Зрозуміло, що потрібно починати з випадку, коли =2. Але якщо =2, то вихідне рівняння взагалі не має розв’язку.
Якщо ≠ 2, то дане рівняння – квадратне, і здавалося б, шукане значення параметра – це корені дискримінанта. Але дискримінант перетворюється в нуль, якщо = 2 або = 5. Оскільки ми встановили, що = 2 не підходить, то = 5.
Відповідь. = 5
Приклад 18.При яких значеннях рівняння ( + 3) 2 + (2 +6) - 3 -9 =0 має більше ніж один корінь?
Розв’язання. Використаємо стандартний крок – почнемо з випадків = 0 і = -3.
Якщо = 0, то рівняння має єдиний розв’язок.
Якщо 
,то розв’язком рівняння буде будь – яке дійсне число.
Якщо 
і 
, то, поділивши обидві частини даного рівняння на 
, отримаємо квадратне рівняння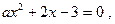 
дискримінант якого 4(1 + 3 ) додатний, якщо 
. З проміжку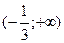 
необхідно виключити точку =0, і не забути включити у відповідь = -3.
Відповідь. = -3, або -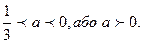 
Приклад 19. При яких значеннях рівняння 
має єдиний розв’язок?
Розв’язання. Дане рівняння рівносильне системі 
Наявність квадратного рівняння і умови єдності розв’язку, очевидно, приведуть до відшукання коренів дискримінанту. Разом з тим умова х ≠0 повинна привернути увагу. І річ у тім, що квадратне рівняння може мати два корені! Але обов’язково тільки один з них повинен дорівнювати -3. Маємо: D= 2 -4, звідки D =0,
якщо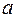 
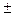= 2; х = -3 буде коренем рівняння 
,
якщо =- 
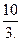, причому при такому значенні другий корінь квадратного рівняння відмінний від – 3.
Відповідь. = 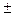2 або = -
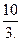
Приклад 20.При яких значеннях рівняння х2- і 
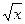- =0
рівносильні?
Розв’язання. Очевидно, якщо 
, то перше рівняння має два різних корені, а друге – тільки один, і в цьому випадку рівняння нерівносильні. Зрозуміло, що якщо =0, то розв’язки рівнянь збігаються. Якщо 0, то ні перше, ні друге рівняння розв’язків не мають. Тому вони рівносильні.
Відповідь. ≤ 0.
Приклад 21.Розв’язати рівняння |ах-1|=|х+3|.
