Чтобы найти наибольшее и наименьшее значения непрерывной на отрезке [ a; b ] функции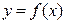 
, нужно:
1. Найти все критические точки, принадлежащие промежутку [ a; b ], и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка [ a; b ], т.е. найти 
и 
.
3. Сравнить все полученные результаты; наибольшее из найденных значений является наибольшим значением функции на отрезке [ a; b ]; аналогично, наименьшее из найденных значений есть наименьшее значение функции на этом отрезке.
Задание 35. Найти наибольшее и наименьшее значения функции 
на отрезке (-3; 4).
Решение: 1. Найдем критические точки функции в промежутке (-3; 4). Имеем 
; решая уравнение 
, получим 
и 
. Эти точки принадлежат данному отрезку (-3; 4).
Вычислим значения функции в критических точках:
2. Находим значения функции на концах отрезка: 
.
3. Сравнивая значения функции в критических точках и её значения на концах отрезка, заключаем, что у = -9 является наименьшим, а у = 40 – наибольшим значением функции на указанном отрезке.
