А.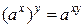 
. При возведении степени в степень показатели степеней перемножаются.
Б. 
.
В. 
. Если основания степеней одинаковы, то при умножении показатели степеней складываются, при делении – показатели степеней вычитаются.
Г. 
Д. 
Е.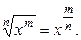 
Например:
.
.
.
.
.
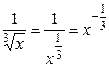Задание 3. Найти производную функции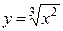 
.
Решение: Сначала преобразуем по формуле Е:
.
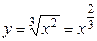Производную этой функции найдем по формуле Х:
.
Задание 4. Найти производную функции 
.
Решение: Сначала преобразуем это выражение по формулам Е, Д, Б:
.
Производную этой функции найдем по формулам V, Х:
.
Производную этого выражения можно найти по формуле VI, а потом преобразовать:
Задание 5. Найти производную функции 
.
Решение:
Сначала преобразовали выражение по формулам Д, Е. Производную вычисляли по формулам III, II, X, затем преобразовали полученное выражение по формулам Д, Е.
Найти самостоятельно производную функции:
2а) 
2б) 
Задание 6. Найти производную функции 
.
Решение:
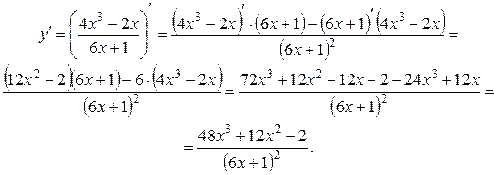
Применили формулу VI. Далее производные находим по формулам III, X, II, I.
Найти самостоятельно производную функции:
3а) 
3б)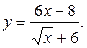 
Задание 7. Найти производную функции 
.
Решение:
Использовали формулу 10, затем формулы III, V, X.
Найти самостоятельно производную функции:
4а) 
.
4а) 
.
Задание 8. Найти производную функции 
.
Подставим это выражение в виде степени:
.
Производную найдем сначала по формуле 10.
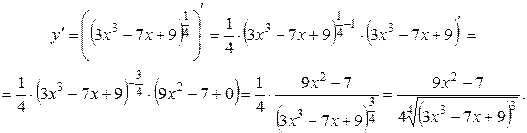
Затем производную находим по формулам III, V, I, X.
Найти самостоятельно производную функции:
5а)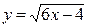 
.
5б) 
.
Задание 9. Найти производную функции 
.
Решение: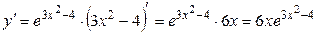 
формула 13, затем формулы III, V, I, X.
Найти самостоятельно производную функции:
6а) 
.
6б) 
.
Задание 10. Найти производную функции 
.
Решение: 
формула 12, затем решаем по формулам 11, III, V, I, X.
Найти самостоятельно производную функции:
7а) 
.
7б)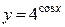 
.
Напомним некоторые формулы действий с логарифмическими функциями:
.
.
.
.
.
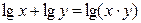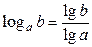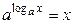Эти формулы верны для любого основания логарифмов.
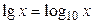
е ≈ 2, 718.
Задание 11. Найти производную функции 
.
Решение:
формула 8.
Найти самостоятельно производную функции:
8а) 
.
8б)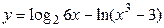 
.
Задание 12. Найти производную функции 
.
Решение: сначала можно преобразовать по формуле логарифма степени:
.
.
Найти самостоятельно производную функции:
9а)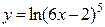 
.
9б)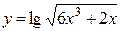 
.
Задание 13. Найти производную функции 
.
Решение: 
- формула 14, V.
Найти самостоятельно производную функции:
10а) 
.
10б) 
.
Задание 14. Найти производную функции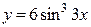 
.
Решение: 
(формулы (V, 10, 14).
Найти самостоятельно производную функции:
11а) 
.
11б) 
.
Задание 15. Найти производную функции 
.
Решение: 
(формулы V, 10, 16).
Найти самостоятельно производную функции:
12а) 
.
12б) 
.
Задание 16. Найти производную функции 
.
Решение:
(формулы IV, XIII, XIV).
Найти самостоятельно производную функции:
13а) 
.
13б) 
.
Задание 17. Найти производную функции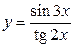 
.
Решение: 
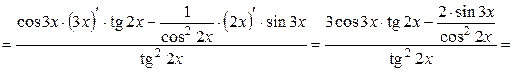
(формулы VI, 14, 16, V).
Найти самостоятельно производную функции:
14а) 
.
14б) 
.
Задание 18. Найти производную функции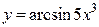 
.
Решение: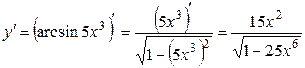 
(формула 18).
Найти самостоятельно производную функции:
15а) 
.
15б) 
.
Задание 19. Найти производную функции 
.
Решение: 
(формула 20).
Найти самостоятельно производную функции:
16а) 
.
16б) 
.
Задание 20. Найти производную функции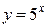 
.
Решение: Используя формулу 
, получим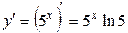 
.
Найти самостоятельно производную функции:
17а)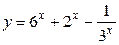 
.
17б)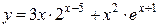 
.
Задание 21. Продифференцировать функцию 
.
Решение: 
(формулы 12, XIII).
Найти самостоятельно производную функции:
18а)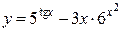 
.
18б) 
.
Производную от данной функции часто называют первой производной (или производной первого порядка). От производной также можно взять производную, которую называют второй производной (или производной второго порядка) и обозначают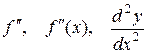 
.
Производной третьего порядка (или третьей производной) называют производную от второй производной. Её обозначают 
.
Например, для функции 
имеем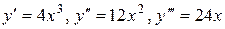 
.
