В интервалах 
и 
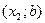данная функция возрастает, а в интервале 
- убывает (рис. 1).
  у
| ||
 
| ||
| ||
| а | х2 | |
  
| 0 х1 х3 b x |
Рис. 1.
Интервалы, на которых функция только возрастает или же только убывает, называются интервалами монотонности функции, а сама функция называется монотонной на этих интервалах.
Если производная функции положительна (отрицательна) в некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).
Задание 32. Найти интервалы монотонности следующих функций: 
.
Решение: Находим производную данной функции: 
. Находим критические точки функции: 
. Область определения функции (-¥; ¥) разбивается на интервалы (-¥; 2) и (2; ¥).
На интервале (-¥; 2) имеем 
; например, 
. Следовательно, на интервале (-¥; 2) функция убывает. На интервале (2; ¥) имеем 
; например, 
. Значит, на интервале (2; ¥) функция возрастает.
