Если аргумент функции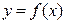 
изменяется от значения х до нового значения х 1, то разность этих значений называют приращением аргумента
D х = х 1 - х.
Сама функция 
при таком изменении аргумента принимает новое значение 
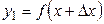, т.е. получим приращение функции 
.
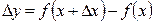Задание 26. Найти приращения аргумента и функции у = 2 х 2 + 1, если аргумент х изменяется от 1 до 1,02.
Решение: Находим приращение аргумента: D х = 1,02 - 1 = 0,02.
Находим значение функции при старом значении аргумента, т.е. при х =1: у =2×12+1=3. Находим значение функции при новом значении аргумента, т.е. при х = 1,02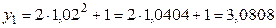 
.
Вычитая из нового первоначальное значение функции, найдем приращение функции: D у = 3,0808 - 3 = 0,0808.
Главная часть приращения функции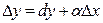 
, линейная относительно приращения независимой переменной, называется дифференциалом функции и обозначается знаком 
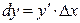, дифференциал функции можно вычислить по формуле
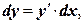
где 
- приращение функции, dy – дифференциал функции, а 
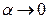при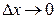 
, 
.
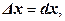Например, если 
, то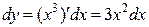 
, если 
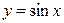, то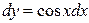 
.
приближенное значение приращения функции совпадает с её дифференциалом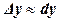 
, что применяется для приближенных вычислений.
Пусть теперь дана функция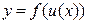 
, которая косвенно зависит от х через другую зависимую переменную и (например, 
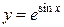или 
и подобные), т.е.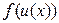 
- функция от функции, или сложная функция.
.
.
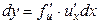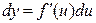Например, для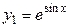 
получим 
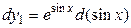; для 
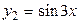получим 
.
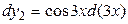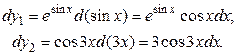
Задание 27. Найти приращение и дифференциал функции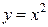 
в точке 
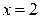при D х = 0,1.
Решение: Приращение функции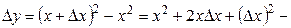 
.
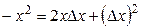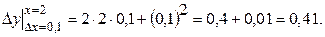Приращение функции 
.
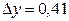Найдем дифференциал функции 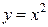, где D х = dx.
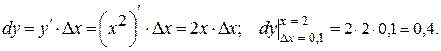
Дифференциал функции равен dy = 0,4.
Задание 28. Пользуясь понятием дифференциала функции, вычислить приближенно изменение функции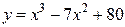 
при изменении аргумента х от 5 до 5,01.
Решение: Находим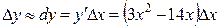 
.
При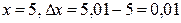 
получим
.
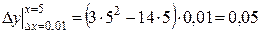Задание 29. Найти абсолютную и относительную погрешности при замене приращения функции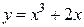 
её дифференциалом в точке 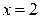при D х = 0,1.
Решение: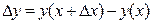 
;
;
;
.
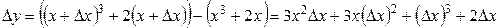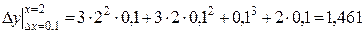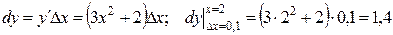Задание 30. С помощью дифференциала вычислить с точностью до 0,01 приращение функци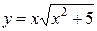и 
при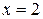 
и D х = 0,2.
Решение: Находим дифференциал данной функции:
.
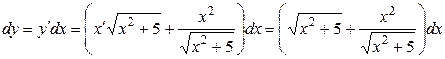При 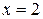и D х = 0,2 получим
.
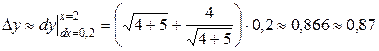Задание 31. Найти дифференциал функции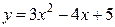 
.
Решение: По формуле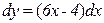 
.
