Если х = а - точка экстремума функции 
, то касательная (в том случае, когда она существует) к графику этой функции в точке 
параллельна оси 0 х (рис. 2).
| у максимум 
| |
  
| ||
| ||
 
| минимум 
| |
| 0 а b х | |
| Рис. 2 |
Правило нахождения точек экстремума:
1. Находят производную 
.
2. Находят все критические точки из области определения функции.
3. Устанавливают знаки производной функции при переходе через критические точки и выписывают точки экстремума.
4. Вычисляют значения функции 
в каждой экстремальной точке.
Задание 33. Исследовать на экстремум функцию: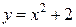 
.
Решение: 1. Находим производную: 
.
2. Приравниваем её нулю 2 х = 0, откуда х = 0 – критическая точка.
3. Определяем знак производной при значении x < 0, например, при 
. Определяем знак производной при x > 0, например, при 
. Так как при переходе через х = 0 производная изменяет знак с минуса на плюс, при х = 0 функция имеет минимум.
4. Находим минимальное значение функции, т.е. 
. Теперь можно на чертеже изобразить вид кривой вблизи точки А (0;2) (рис. 3).
 у
|
|
|
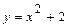
| А(0;2) |
  
|
| 01 х |
| Рис. 3 |
Задание 34. 
. Исследовать на экстремум, найти интервалы монотонности функции.
Решение: 1. Находим производную:
.
2. Находим критические точки: 
.
3. Исследуем знаки производной слева и справа от критической точки: 
.
Следовательно, при 
функция имеет минимум 
.
Результаты можно отразить в таблице:
| х | (-¥; -1) | -1 | (-1; ¥) |
| - | + | |
| у | убывает | у min= -1/ е | возрастает |
