.
Уравнение нормали к кривой 
в точке 
имеет вид:
, где 
.
Задание 22. Составить уравнения касательной и нормали к графику функции 
в точке с абсциссой 
.
Решение: Найдем значение функции при 
: 
. 
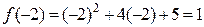Найдем производную данной функции: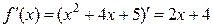 
, вычисляем значение производной при , 
.
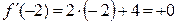Подставив эти значения в формулы, получим уравнения касательной и нормали в точке .
Уравнение касательной: 
, откуда 
.
В данном случае касательная параллельна оси 0Х.
Уравнение нормали найдем не по формуле, а как уравнение прямой, перпендикулярной оси 0Х. Ее уравнение .
19а) Найти самостоятельно уравнение нормали и касательной к графику функции 
в точках пересечения с осью 0 х.
Задание 23. Кривая задана уравнением 
. Определить угол наклона касательной к положительному направлению оси 0 х, проведенной к кривой в точке с абсциссой .
Решение: Найдем производную: 
. Обозначив угол наклона касательной в точке с абсциссой 
через a, получим 
(–2),
, 
откуда a = p¤4 (или в градусной мере a = 45°).
Угловой коэффициент касательной к графику функции y = f (x) в точке х 0 равен значению производной функции y = f (x), вычисленной для х 0
.
Угловой коэффициент прямой равен тангенсу угла наклона прямой
.
Уравнение прямой 
где k – угловой коэффициент.
Задание 24. На кривой 
найти точку, в которой касательная: а) параллельна прямой 
; б) перпендикулярна прямой 
.
Решение: Пусть искомая точка касания есть 
. Тогда, как известно, угловой коэффициент k касательной равен значению производной в точке касания, т.е.
.
Учитывая это, рассмотрим каждое из условий задачи.
а) Для того, чтобы касательная была параллельна прямой 
, их угловые коэффициенты должны совпадать, т.е. k = 2 или 
. Решая последнее уравнение относительно 
, получим: 
. Подставляя найденное значение абсциссы искомой точки в уравнение кривой, найдем значение её ординаты: 
. Итак, 
- искомая точка.
б) Из аналитической геометрии известно, что угловые коэффициенты взаимно перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. Так как угловой коэффициент прямой 
равен 
, то угловой коэффициент k искомой касательной равен –4, и мы имеем уравнение 
, откуда 
, т.е. 
. Соответственно находим 
. Следовательно, точка 
- искомая.
