В1. К графику заданной функции у = 
проведите касательную так, чтобы она была параллельна прямой у = 2 –х.
В2. На рисунке изображен график производной функции у = f '(x), заданной на отрезке [-6; 3]. Исследуйте функцию у = f(x) на монотонность и укажите в ответе длину промежутка возрастания.
У
y=f ‘(x)
| |
 |
О 1 х
В3. Найти точки экстремума функции y =3 х 4-16 х 3+24 х 2-11.
Запишите решение заданий уровня С с полным обоснованием
С1. Найдите все значения a, при которых функция y = 
имеет минимум в точке x 0=3.
С2. Решите графически уравнение 3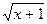 
= - x 3 + 3 x 2 +6
Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 6
Запишите вариант правильного ответа заданий уровня А
A1. Найдите производную функции f (x)= x 6+ cosx
а) 6 х 5-sin x б) 
- sinx в) 6 x 5+ sinx г) 
+ sinx
A2. Найдите производную функции y =7 x 2-2 x +4
а) 14 x -2 б) 7· 
-2 в) 14 x +2 г) 7 x +4
A3. Найдите производную функции y =-5+ ctgx
а) 
б) - в)-5- г)-5+ 
A4. Найдите производную функции y = 
в точке x 0=0.
а)-2 б)4 в)1 г)-3
A5. Найдите угловой коэффициент касательной к графику функции
y =15 x -20 cosx в точке с абсциссой x 0= - 
.
а) 20-15 
б) 
в) -5 г) 15
A6. Решите уравнение f´ (x)=0,если f (x)=(3 x 2+1)·(3 x 2-1)
а) - 
б) в) 0 г) 
A7. Прямолинейное движение точки описывается законом S=t 4-2 t 2 (м) Найдите её скорость в момент времени t =3 с.
а) 0 б) 98 в) 96 г) 92
A8. Найдите скорость изменения функции y =23 x -175 в произвольной точке x
а) 175 б) 23 в) 198 г) 0
A9. Найдите промежутки убывания функции y = x 3-6 x 2+5
а) [-4;0] б) (-∞;0] 
[4;+ ∞) в) [0;4] г) нет таких промежутков 
А10. Найдите промежутки возрастания функции f (x)= 
а)(-∞;0,25) (
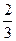;+ ∞) б) (-∞;0,25) (0,25;+ ∞) в)(-0,25;0,25) г)(- 
;0,25] [0,25; + )
А11. Составьте уравнение касательной к графику функции y = 2- x - x 3 в точке с абсциссой x 0=0.
а) y =- x -2 б) y = x -2 в) y =2- x г) y = x +2
А12. Найдите все значения x, при которых выполняется неравенство
f (x) 
,если f (x)=7,5 x 2- x 3.
а) (-∞;-5] [0;+ ∞) б) (-∞;0) (5;+ ∞) в) [0;5] г) (0;5)
