По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 3
Запишите вариант правильного ответа заданий уровня А
А1. На рисунке изображен график функции у=f(x). Укажите число точек экстремумов.
| а) 1 б) 2 в) 3 г) 4 |
А2. Укажите производную функции у= х 4 -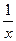 
.
а) 4 х - 
| б) 4 х 3-
| в) 4 х 3+
| г) 4 х +
|
А3. Найдите f ' (16), если f (x)=8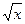 
-3.
а) 3 б) 2 в) -1 г) 1
А4. Найдите производную функции у =3 х 2 cosx.
а) y '= - 6 x sinx б) y '=6 xcosx -3 x 2 sinx
в) y '= x 3 cosx +3 x 2 sinx г) y '=6 xcosx +3 x 2 sinx
А5. Найдите минимум функции у=х 3-3 х +2.
а)-1 б) 0 в) 1 г) 4
А6. Укажите, какая из функций убывает на всей координатной прямой.
а) у=х 3+ х б) у=х 3- х в) у= -х 3- х г) у= -х 2+1
А7. Найдите производную функции у =(-3+6 х)7.
а) y '=42(-3+6 x)6 б) y '= -21(-3+6 x)6 в) y '= 7(-3+6 x)6 г) y '= -7(-3+6 x)6
А8. Укажите число точек экстремума функции у =4 х - х 4.
а) 0 б) 1 в) 2 г) 3
А9. Найдите угловой коэффициент касательной, проведенной к графику функции f (x)=4 х 3-6 х 2+9 через его точку с абсциссой х 0=1.
а)1 б) 2 в) 0 г) -1
А10. Найдите момент остановки тела, движущегося по закону S (t)= t 2-6 t -16.
а) 8 б) -2 в) -3 г) 3
А11. Найдите наименьшее значение функции у=2 х 3-6 х на отрезке [0;2].
а) -6 б) -4 в) -2 г) 0.
А12. Найдите тангенс угла наклона касательной, проведенной к графику функции у = - 
в его точке с абсциссой х 0= -2.
а) 1 б) 2 в) 0 г) -1.
