Диагностическая контрольная работа
По алгебре и началам анализа
«Производная функции. Приложения производной»
Вариант 1
Запишите вариант правильного ответа заданий уровня А
А1. Найдите производную функции y=9 - 9x8 - 
x5
а)9 x - x 9-  x 6
| б)9 x -72 x 7-5 x 4 | в)-72 x 7-6 x 4 | г)-17 x 7-6 x 4 |
А2. Найдите производную функции y=(4-3x)5 .
| а)20(4-3 x)4 | б)5(4-3 x)4 | в)-15(4-3 x)4 | г)-5(4-3 x)4 |
А3. Укажите функцию, являющуюся первообразной для функции f (x)= 
, при x >0.
а)- 
| б)
| в)2 lnx | г) ln 2x |
А4. Найдите производную функции f(x)=xcos x.
| а) cos x | б) -sin x | в) cos x + x · sin x | г) cos x - x · sin x |
А5. Найдите значение производной функции f (x)=3 x 2-6 lnx в точке x 0=1.
| а) 6 | б) 0 | в) 3 | г) -3 |
А6. Найдите значение производной функции f(x)= x 2 sin x в точке x 0= 
.
а)- 
| б)
| в)-2
| г)2
|
А7. Найдите угловой коэффициент касательной к графику функции
f(x)= 
x3-2x+7 в точке с абсциссой x 0=3.
| а) 7 | б) 18.75 | в) 10 | г) -1 |
А8. Найдите тангенс угла наклона касательной к графику функции y = x 4+sin x в точке с абсциссой равной 2.
| а)32+ cos 2 | б)32- cos 2 | в)16 ln 2+cos2 | г)2 cosx - 
|
А9. Значение функции y=x3-2x2-4x-1 в точке минимума равняется
а)-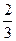 
| б)2 | в)-9 | г)- 
|
А10. Найдите наименьшее значение функции y= 
-x2-3x-1 на отрезке [-3;1].
| а) -3 | б)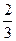
| в) -10 | г) -12 |
А11. Найдите площадь фигуры, ограниченной линиями x=0, x=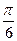 
, y=0, y=cos x.
а) 
| б) 
| в)1-
| г) 
|
А12. Сколько экстремумов имеет функция у= 
- +5х 
-1?
| а) 2 | б) 0 | в) 1 | г) 3 |
Запишите решение заданий уровня В с полным обоснованием
В1. Точка движется по координатной прямой согласно закону х(t)=-5+7t-е 
, где х(t) – координата точки в момент времени t. Найдите скорость точки при t=3.
В2. Функция у=f(x) задана на промежутке (-5;5). График ее производной
у= 
(х) изображен на рисунке. Определите наибольшее из тех значений х, при которых функция имеет минимум.
В3. Для функции f(х)= 
+х +х 
найдите первообразную, график которой проходит через точку (1;3).
