Гладкость функции  зависит от скорости стремления к нулю
зависит от скорости стремления к нулю 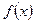 при
при  . Пусть интегрируемым является произведение
. Пусть интегрируемым является произведение  – фиксированная постоянная.
– фиксированная постоянная.
По определению  для
для  . Определим этим же равенством функцию комплексного аргумента
. Определим этим же равенством функцию комплексного аргумента  :
:

Этот интеграл сходится в полосе  , так как
, так как  и
и  для всех действительных
для всех действительных 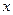
 .
.
Утверждение.  – аналитическая функция комплексного переменного
– аналитическая функция комплексного переменного  в полосе
в полосе  . При
. При  эта функция стремится к нулю равномерно по
эта функция стремится к нулю равномерно по  .
.
Доказательство. В каждой внутренней точке полосы эта функция комплексного аргумента  дифференцируема: при формальном дифференцировании по
дифференцируема: при формальном дифференцировании по  имеем
имеем

этот интеграл равномерно сходится в некоторой окрестности точки  (не выходящей за пределы полосы) и представляет, следовательно, производную функции
(не выходящей за пределы полосы) и представляет, следовательно, производную функции  . Функция
. Функция  ограничена во всей указанной полосе:
ограничена во всей указанной полосе:

Отсюда следует, в частности, что последовательности функций  , сходящейся по
, сходящейся по  отвечает последовательность
отвечает последовательность  , равномерно сходящаяся во всей полосе
, равномерно сходящаяся во всей полосе  .
.
Далее, можно утверждать, что функция  стремится при
стремится при  к нулю равномерно по
к нулю равномерно по  ,
,  . Действительно, это имеет место для преобразования Фурье характеристической функции интервала
. Действительно, это имеет место для преобразования Фурье характеристической функции интервала  :
:
 ,
,
поскольку числитель полученного выражения ограничен при  (
( ). К общему случаю можно перейти обычным предельным переходом от ступенчатых функций.
). К общему случаю можно перейти обычным предельным переходом от ступенчатых функций.
Утверждение доказано.
Отметим, что в силу последнего свойства в формуле обращения можно произвести интегрирование не только по вещественной оси, но по любой параллельной прямой, лежащей в указанной полосе  -плоскости, так что
-плоскости, так что

В приложениях иногда приходится применять преобразования Фурье к функциям, имеющим разное асимптотическое поведение при 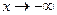 и
и  .
.
Теорема. Пусть 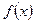 – локально абсолютно интегрируемая функция вещественного аргумента
– локально абсолютно интегрируемая функция вещественного аргумента 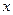 такая, что
такая, что 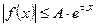 при
при 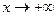 и
и  при
при 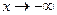 , причём
, причём  . Тогда интеграл
. Тогда интеграл

определяет аналитическую функцию  от
от  в полосе
в полосе  . При любом
. При любом  имеет место формула обращения
имеет место формула обращения
 ,
,
если только она имеет место хотя бы для одного 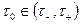 .
.
Замечание. В приведенной ниже теореме доказано, что формула обращения имеет место для любого  .
.
Доказательство. Сходимость интегралов от  и от
и от  в полосе
в полосе  следует из локальной интегрируемости
следует из локальной интегрируемости  и оценок при
и оценок при 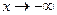 и
и  :
:
 при
при 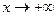 , так как
, так как  ,
,
 при
при 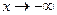 так как
так как  .
.
Стремление к нулю при 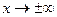 сохраняется при умножении экспонент на
сохраняется при умножении экспонент на 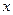 .
.
Убедимся в справедливости формулы обращения, для чего подставим в неё 


Возможность обращения преобразования Фурье на функции  при любом
при любом 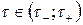 вытекает из предположения о его обратимости при
вытекает из предположения о его обратимости при  , так как
, так как  в силу теоремы Коши и равномерного по
в силу теоремы Коши и равномерного по  стремления к нулю функции
стремления к нулю функции  .
.
Теорема доказана.
Переход к комплексным значениям аргумента  образа преобразования Фурье позволяет применять его к функциям вещественного аргумента, которые на всей вещественной оси могут быть неинтегрируемыми.
образа преобразования Фурье позволяет применять его к функциям вещественного аргумента, которые на всей вещественной оси могут быть неинтегрируемыми.






