Предположим, что абсолютно интегрируемая функция f(x) абсолютно непрерывна в окрестности каждой точки и её производная также абсолютно интегрируема на оси -∞<x<∞. Выясним, как связаны преобразования Фурье функции f(x) с её производной.
Заметим, что из интегрируемости 
следует существование предела функции 
при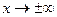 
. Этот предел может быть только нулём, так как иначе f(x) не была бы интегрируемой. Интегрированием по частям получаем 
.
По доказанному, внеинтегральный член равен нулю. Получаем равенство
.
Если у функции f(x) интегрируемы производные до порядка m, то, повторяя процесс, получаем,
k=0,1,..,m.
Так как, как 
преобразование Фурье интегрируемой функции есть ограниченная функция от 
(и даже стремящаяся к 0, при 
), то
.
Итак, чем больше функция f(x) имеет интегрируемых производных, тем быстрее её преобразования Фурье стремятся к нулю на бесконечности.
Замечание. В частности, при некоторой гладкости функции f(x) её преобразование Фурье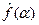 
становится также абсолютно интегрируемой функцией. Из полученного неравенства видно, что для этого достаточно существования в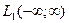 
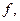
и 
. Можно ограничиться существованием 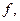и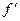 
, но при дополнительном условии, что они принадлежат не только 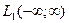, но и 
. В этом случае из 
следует 
, откуда
.
Для любого линейного дифференциального оператора 
с постоянными коэффициентами порядка ≤ m получаем
.
Линейное дифференциальное уравнение на оси 
относительно функции f(x) переходит в алгебраическое уравнение на оси 
относительно 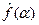.Это открывает новые возможности для решения дифференциальных уравнений. Поскольку дифференциальные уравнения, к которым можно применить этот метод должны быть линейными с постоянными коэффициентами, то для обыкновенных дифференциальных уравнений этот метод мало что даёт (учитывая, тем более, что мы должны оставаться в границах класса интегрируемых на всей оси функций). Но для уравнений с частными производными метод преобразования Фурье уже оказывается полезным.
