Знаем, что преобразование Фурье абсолютно интегрируемой функции 
есть ограниченная непрерывная функция 
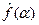, стремящаяся к нулю при 
. Предположим теперь, что не только 
, но и 
. Тогда можно утверждать, что функция 
дифференцируема. Действительно, формальное дифференцирование по параметру 
интеграла Фурье 
приводит к интегралу 
, который является абсолютно сходящимся и равномерно сходящимся по параметру . В силу теоремы о дифференцировании интеграла Лебега по параметру функция дифференцируема и производная равна , то есть
.
Производная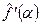 
– преобразование Фурье интегрируемой функции, поэтому 
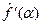снова непрерывна, ограничена и стремится к нулю при .
Если вместе с функцией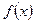 
абсолютно интегрируемыми на оси 
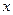являются также функции 
, 
,…, 
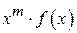, то процесс дифференцирования можно продолжить. Мы получим, что функция 
имеет производные до порядка m, непрерывные, ограниченные и стремящиеся к нулю при . При этом имеет место формула 
, 
Для произвольного многочлена 
степени 
.
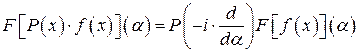Видим, что чем более сильные условия убывания на бесконечности наложены на функцию 
, тем более гладкой получается функция 
.
В связи с изложенным можно указать важный класс функций, который при преобразовании Фурье переходит в самого себя, только с заменой аргумент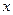а на . Рассмотрим совокупность 
бесконечно дифференцируемых функций 
, которые для всех 
удовлетворяют неравенствам 
,где 
‑ постоянная, зависящая от выбора функции 
. Через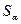 
обозначим класс таких же функций 
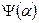аргумента .
Заметим прежде всего, что при любых целых неотрицательных k и q произведение 
, так как 
.
Пусть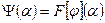 
. По доказанному 
, причём 
. Функция 
и все её последовательные производные интегрируемы, поскольку линейно выражаются через интегрируемые функции 
. Поэтому функции 
ограничены при всех 
и 
как преобразования Фурье интегрируемых функций (в последнем равенстве использованы два свойства преобразования Фурье: 
и 
).
Итак, если принадлежит , то 
. Обратно, пусть 
. Построим функцию 
. Функция 
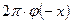есть, очевидно, преобразование Фурье функции 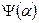и поэтому входит в . Но тогда, очевидно, и 
. По формуле обращения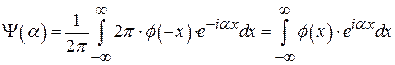 
(функции из удовлетворяют условию Дини в каждой точке).
Итак, каждая функция есть преобразование Фурье функции 
(причём 
).
Таким образом, при преобразовании Фурье класс отображается на весь класс . Символически этот факт можно записать равенством 
.
