Когда мы желаем представить периодическую функцию f(x) с периодом 
в виде наложения чистых гармонических колебаний, мы обращаемся к ряду Фурье:
Если речь идет о функции с периодом 
, то соответствующий ряд Фурье приобретает вид
, где 
.
Из двух последних равенств следует
.
Формальный переход к пределу при 
приводит к формуле
,
где символом 
обозначен непрерывный аргумент, получающийся из дискретного аргумента 
.
Итак, для функции f(x), определенной на всей числовой оси 
, искомая формула представления в виде наложения гармонических колебаний должна иметь вид
(1)
где 
. (2)
Функция 
, определяемая равенством (2) называется преобразованием Фурье функции f(x). Формула (1) называется формулой обращения преобразования Фурье или обратным преобразованием Фурье.
Покажем, что из (2) следует (1) при определенных предположениях относительно функции f(x).
Первое предположение состоит, естественно, в том, что функция f(x) интегрируема на всей оси . Это обеспечивает существование интеграла (2) при любом значении 
.
Утверждение. Если 
, то – ограниченная, непрерывная при всех 
функция и при 
она стремится к нулю.
Доказательство.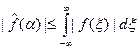 
. Из этой оценки вытекает, что последовательность функций 
, сходящаяся по норме пространства 
переводится преобразованием Фурье в последовательность функций 
, равномерно сходящуюся на всей оси 
.
Второе и третье утверждения проверим сначала для характеристической функции интервала (c,d): 
– непрерывная функция и стремится к нулю при . Далее, любая ступенчатая функция является линейной комбинацией характеристических функций интервалов, любая суммируемая функция есть предел по норме последовательности ступенчатых. По доказанному ее преобразование Фурье есть равномерный предел на оси 
, непрерывных функций, стремящихся к нулю на бесконечности.
Утверждение доказано.
Теперь обратимся к доказательству формулы (1). Рассмотрим сначала интеграл в конечных пределах 
Внутренний интеграл сходится равномерно по параметру : 
и его оценка не зависит от . Внешний интеграл от ограниченной функции в конечных пределах сходится. В силу следствия теоремы Фубини для неотрицательных функций существует двойной интеграл Лебега, который равен обоим повторным. Поэтому можно поменять порядок интегрирования:
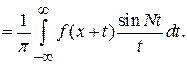
Теорема. Если функция f в точке x удовлетворяет условию Дини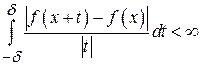 
при некотором 
, то 
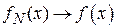при 
.
Доказательство. Из курса математического анализа должно быть известно равенство 
. Поэтому справедливо равенство
.
Интеграл разобьем на две части 
. Второе слагаемое можно записать в виде
.
Отсюда видно, что при данном x и заданном большом значении T это слагаемое делается как угодно малым независимо от значения N.
Первое слагаемое имеет вид
и, так как функция 
в заданном промежутке суммируемая по t (условие Дини), то это слагаемое стремится к нулю с возрастанием N по лемме, доказанной в процессе доказательства аналогичной теоремы о сходимости тригонометрического ряда Фурье.
Теорема доказана.
Итак, если функция 
и удовлетворяет в точке x условию Дини, то её значение 
восстанавливается по преобразованию Фурье 
.
Подчеркнём, что интеграл (1) (обратное преобразование Фурье) не является, вообще говоря, абсолютно сходящимся и не может быть определен как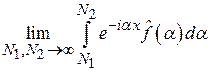 
.
