Рассмотрим применение преобразования Фурье для решения дифференциальной задачи в частных производных на примере задачи Коши для однородного уравнения теплопроводности
, 
-∞ < x < ∞, 
,
.
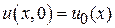Чтобы применить к этой задаче классическое преобразование Фурье, мы должны предположить, что эта задача имеет решение, которое удовлетворяет следующим условиям:
а) при любом фиксированном 
, 
, 
;
б) функция 
имеет в каждом интервале 
интегрируемую мажоранту
Последнее условие гарантирует корректность дифференцирования по параметру t под знаком интеграла функции 
. Применим к уравнению теплопроводности преобразование Фурье:
, 
, ,
.
Решение полученного обыкновенного дифференциального уравнения при заданном начальном условии хорошо знакомо: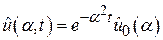 
. Мы знаем, что 
, 
. Отсюда при 
имеем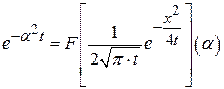 
.
По формуле свертки
,
и так как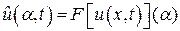 
, то окончательно
.
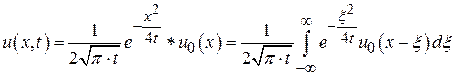Полученная формула решения называется интегралом Пуассона.
