и 
- это источники поля. Рассмотрим поле на больших расстояниях.
Считаем, что выполнено условие:
чем более точно оно выполнено, тем меньше нам нужно брать слагаемых в разложении. Запишем:
,
где 
- малый параметр, по которому производится разложение.
Разложим подынтегральные функции из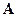 
и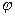 
в ряд Тейлора:
здесь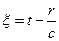 
, 
, 
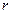от переменной интегрирования не зависят.
Рассмотрим 
.
Здесь интегрирование ведется по всему объему системы с характерным размером 
.
- потенциал кулоновского типа
Зависимость 
- фиктивная, т.е. 
. Обычно часть 
не рассматривают, т.к. здесь не происходит излучения. Для излучения заряд должен двигаться ускоренно.
Дипольный момент зависит явно от переменной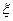 
, т.к. он берется в определенный момент времени (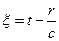). Тогда дипольный момент есть функция времени и координат.
Интересно, что 
и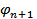 
связаны между собой калибровкой Лоренца.
