Теорема может быть выведена с помощью двух уравнений Максвелла (для простоты считаем, что среда - вакуум (μ=1, ε=1); для общего случая с произвольной средой, нужно в формулы к каждому ε0 и μ0 приписать ε и μ):
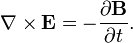
Домножив обе части уравнения на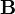 
, получим:
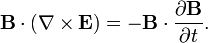
Рассмотрим сначала уравнение Максвелла-Ампера:
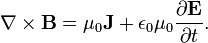
Домножив обе части уравнения на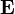 
, получим:
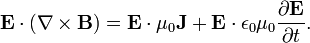
Вычитая первое из второго, получим:
Наконец:
Поскольку вектор Пойнтинга 
определяется как:
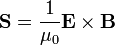
это равносильно:
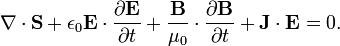
Теорема Пойнтинга (англ. Poynting's theorem) — теорема, описывающая закон сохранения энергии электромагнитного поля. Теорема была доказана в 1884 Джоном Генри Пойнтингом. Всё сводится к следующей формуле:
,
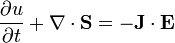Где S — вектор Пойнтинга, J — плотность тока и E — электрическое поле. Плотность энергии 
(
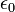— электрическая постоянная, 
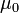— магнитная постоянная).
38. Доказательство закона сохранения энергии для системы: электромагнитное поле + заряженные частицы.
Максвелловский тензор напряжений в вакууме и в среде. Инвариантность относительно дуальных преобразований.
