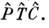Уравнения Максвелла в вакууме в векторной дифференциальной и интегральной формах в присутствии магнитных источников. Сила Лоренца для магнитного заряда.
Дуальная симметрия уравнений Максвелла для электромагнитного поля и в присутствии электрического и магнитного зарядов. Инвариантность выражений для энергии и импульса электромагнитного поля относительно дуальных преобразований.
Двойственная симметрия M. у. имеет место для любой формы их записи. Она состоит в инвариантности M. у. относительно линейных преобразований нолей, производимых по след, правилам:
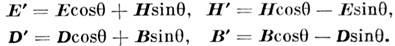
Здесь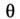 
- произвольный угл. параметр; в частности, при 
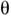= О получаются тождественные преобразования, а при 
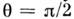- стандартные преобразования перестановочной двойственности (операция 
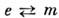): замена 
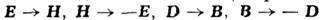даёт в областях, свободных от источников, новое решение M. у. При этом, однако, оно меняет местами ур-ния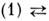 
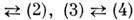и, следовательно, там, где раньше были распределены электрич. источники, возникают источники магнитные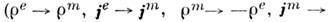 
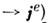. Поэтому с точки зрения двойственной симметрии M. у. задание материальных связей в виде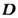 
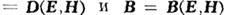представляется вполне удобным. Дуально-симметричные M. у. обладают рядом достоинств, по крайней мере в чисто методич. плане. Так, напр., они симметризуют скачки тангенциальных компонентов магн. и электрич. полей и, если задание ffTall на поверхности идеальной электрич. стенки эквивалентно заданию поверхностного электрич. тока, то задание Я1а„ на идеальной магн. стенке сводится к заданию магн. поверхностного тока: Таким сведением задач с заданными 
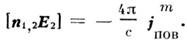полями к задачам с заданными токами широко пользуются в теории дифракции волн, в частности в дифракции радиоволн. Принцип перестановочной двойственности является представителем класса дискретных преобразований (см. Симметрия),оставляющих инвариантными M. у. Такого же сорта преобразованиями являются, в частности, операция обращения времени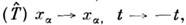 
любые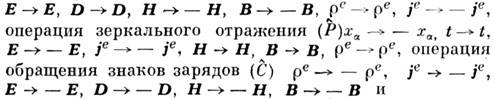 
последовательно осуществляемые комбинации операций 
