Уравнения (68) и (69) можно записать в более удобном виде воспользовавшись отмеченной выше калибровочной инвариантностью потенциалов. При этом, если использовать условие калибровки Лоренца (70), то из уравнений (68) и (69) получим неоднородные волновые уравнения д'Аламбера:
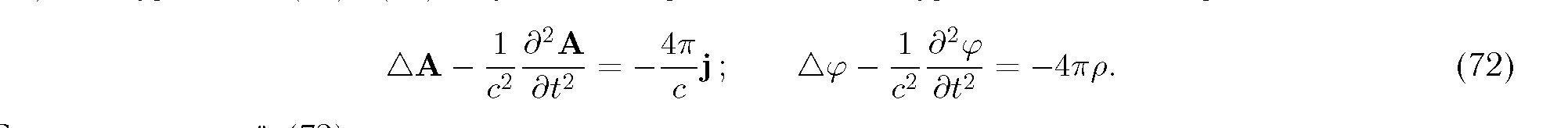
Система уравнений (72) совместно с определениями векторного и скалярного потенциалов полностью эквивалентна системе уравнений Максвелла и решение этой системы при отсутствии специальных граничных условий можно выписать при произвольных р и j:
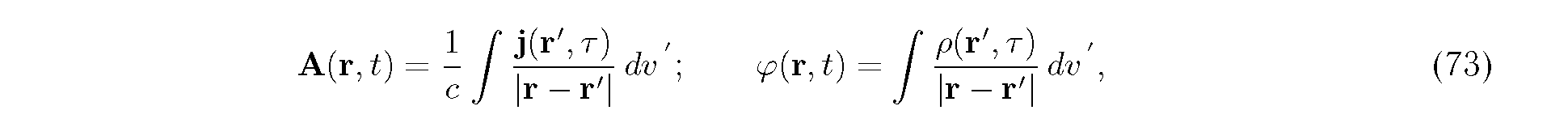
где т = t— |r—r'|/c. Решения неоднородных волновых уравнений (72) вида (73) называются запаздывающими потенциалами, так как значение поля в точке r в момент времени t определяется распределением зарядов и токов в предшествующие моменты времени. Это соответствует принципу причинности в физике. Уравнения (72) имеют также отличные от нуля решения вида(73) в которых т = t + |r - r'|/c. Такие решения называются опережающими и так как они не соответствуют принципу причинности в физических решениях опускаются.






