Известно, что электрические заряды создают в пространстве электрические поля. Если заряды находятся в движении, то эти поля меняются во времени; кроме того, движущиеся заряды создают магнитные поля. Если движения зарядов являются колебательными, то и создаваемые зарядами поля также колеблются во времени и в пространстве, причем эти возмущения полей распространяются с конечной скоростью (скоростью света), то есть происходит распространение электромагнитных волн. Колебания зарядов в природе в большинстве случаев являются гармоническими, то есть синусоидальными, или близкими к синусоидальным. Мы знаем, что синусоидальные колебания возникают, когда смещение чего-либо от положения равновесия пропорционально возвращающей силе; при малых возмущениях эта линейная связь работает почти всегда. Наш электрический мир не является статичным, большинство зарядов в квазинейтральных системах постоянно колеблется вблизи равновесного положения.
Когда мы писали волновое уравнение для упругих сред, мы нигде не использовали для его составления источник волн, молчаливо полагая, если есть волна, то значит, что-то её создало. Волны, возникнув, существуют уже независимо от своего источника; даже если он исчезнет, созданная им волна продолжит свой путь в пространстве. Поэтому волновое уравнение описывает только волну, но никак не её источник.
Поступим также с электромагнитными волнами. Нас будут интересовать сами волны, а не источники, которые их когда-то создали и, может, давно уже исчезли. Напишем основные уравнения электродинамики - уравнения Максвелла для области пространства, занятой волнами, где нет накаких источников - зарядов и токов.
Иными словами, уберём из этих уравнений все заряды и токи. Для однородной и изотропной среды, не обладающей ферромагнитными и сегнетоэлектрическими свойствами (такая среда называется линейной, поскольку выполняется линейная связь между напряженностью и индукцией электрического и магнитного полей соответственно), получим:




Путём чисто математических преобразований, без каких-либо дополнительных предположений эти уравнения приводятся к виду:
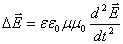
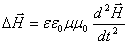
А это есть ни что иное, как волновые уравнения для векторов напряженности электрического и магнитного полей. Мы знаем, что коэффициент в правой части уравнений есть обратный квадрат фазовой скорости волны; отсюда сразу находим эту скорость:

В вакууме e = m = 1, откуда получаем результат, весьма озадачивший современников Максвелла: скорость распространения электромагнитных волн в вакууме есть константа, не зависящая от системы отсчета (уравнения Максвелла, как известно, не инвариантны к преобразованиям Галилея):

Общее решение волнового уравнения нам известно. Частный случай этого решения - синусоидальные волны. Особенность электромагнитных волн в том, что решения для E и H дают одну волну с двумя составляющими; кроме того, колеблющиеся величины - векторные. Далее дадим краткую сводку свойств электромагнитных волн, непосредственно следующих из решения векторных волновых уравнений.




