Фазовая модуляция света. Эффект Поккельса нашел широкое применение при создании различных технических устройств и приборов: оптических волноводов, модуляторов, дефлекторов, затворов и т.п. Наиболее простым из них является фазовый модулятор (модулятор света - устройство для управления параметрами световых потоков: амплитудой, частотой, фазой, поляризацией), в котором линейное электрооп- тическое изменение показателя преломления приводит к фазовому сдвигу распространяющейся волноводной моды.
Волна вида (39), прошедшая путь L в кристалле, помещенном в
электрическое поле  , приобретает фазовый сдвиг
, приобретает фазовый сдвиг

| (62) |
где для  и
и  согласно (41), (57) и (61) имеем:
согласно (41), (57) и (61) имеем:

| (63) |
Здесь  - фазовый сдвиг, приобретенный светом при прохождении пути L в естественном кристалле (в отсутствие поля
- фазовый сдвиг, приобретенный светом при прохождении пути L в естественном кристалле (в отсутствие поля  );
);  - дополнительный фазовый сдвиг, индуцированный полем
- дополнительный фазовый сдвиг, индуцированный полем  . Показатель преломления
. Показатель преломления  и постоянная Поккельса R в (63) выбраны в соответствии с заданными направлениями: распространения волны m, поляризации
и постоянная Поккельса R в (63) выбраны в соответствии с заданными направлениями: распространения волны m, поляризации
поля d и внешнего поля  (подобно тому, как это сделано в (61)).
(подобно тому, как это сделано в (61)).
Наличие фазового сдвига в (63) означает фазовую модуляцию света. Величину  можно записать в виде
можно записать в виде

| (64) |
где V - внешнее напряжение, приложенное к кристаллу; G - размер
кристаллического элемента вдоль силовых линий поля  . Напряжение
. Напряжение  (иногда вместо
(иногда вместо 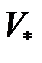 пишут
пишут  ) - так называемое полуволновое напряжение, т.е. напряжение, которое нужно приложить к фазовому модулятору для получения сдвига
) - так называемое полуволновое напряжение, т.е. напряжение, которое нужно приложить к фазовому модулятору для получения сдвига  .
.
При использовании продольного эффекта (G = L)  зависит лишь от
зависит лишь от  и свойств кристаллического элемента, а при поперечном эффекте
и свойств кристаллического элемента, а при поперечном эффекте  зависит и от геометрии кристалла.
зависит и от геометрии кристалла.
Схема амплитудного модулятора света с поляризационной ячейкой. Амплитудный модулятор света (АМС) отличается от фазового наличием двух скрещенных ( ) поляризаторов (рис.11), между которыми находится кристалл.
) поляризаторов (рис.11), между которыми находится кристалл.

Рис.11.
Световая волна, поляризованная входным поляризатором (вектор пропускания  ) и имеющая интенсивность света
) и имеющая интенсивность света  , распадается в анизотропном элементе на волны, поляризованные вдоль
, распадается в анизотропном элементе на волны, поляризованные вдоль  и
и  (здесь для удобства индекс
(здесь для удобства индекс  поляризации (48) поставлен внизу). На выходе элемента, согласно (62) и (63), эти волны получают фазовые сдвиги:
поляризации (48) поставлен внизу). На выходе элемента, согласно (62) и (63), эти волны получают фазовые сдвиги:

| (65) |
В результате прохождения через кристалл линейно-поляризо- ванные моды оказываются сдвинутыми по фазе на

| (66) |
Параметр Г играет существенную роль при расчете интенсивности 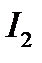 света на выходе поляризатора р2.
света на выходе поляризатора р2.
На рис.12 приведены векторы 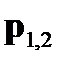 и
и  . Угол
. Угол  определяет связь между следующими амплитудами:
определяет связь между следующими амплитудами: 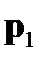 - волны, прошедшей через поляризатор
- волны, прошедшей через поляризатор  ;
;  - линейно-поляризованных мод
- линейно-поляризованных мод  , распространяющихся по кристаллу; Ь\ 2 - составляющих мод d(2, прошедших через поляризатор
, распространяющихся по кристаллу; Ь\ 2 - составляющих мод d(2, прошедших через поляризатор 

Рис. 12.
Из построения следуют равенства:

| (67) |
Для мод  , прошедших через поляризатор
, прошедших через поляризатор  , имеем:
, имеем:

где  . - рассчитанный по формулам (65), (62), (63) фазовый сдвиг
. - рассчитанный по формулам (65), (62), (63) фазовый сдвиг  -й моды. С учетом вытекающего из построений рис. 12 и формул (67) равенства
-й моды. С учетом вытекающего из построений рис. 12 и формул (67) равенства  для суперпозиции волн
для суперпозиции волн  и
и  найдем:
найдем:
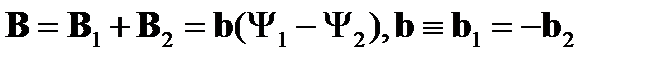
| (68) |
После несложных преобразований для разности  , фазовых множителей будем иметь:
, фазовых множителей будем иметь:

| (69) |
где учтено определение Г, согласно (65). Подставив (69) в (68), получим:

Для достижения на выходе максимальной контрастности полагают  . Тогда в силу (67) запишем:
. Тогда в силу (67) запишем:
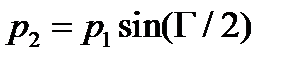
Поскольку интенсивность волны (39) пропорциональна квадрату любого из векторов D 0, E 0, H 0 для интенсивности I2 света, прошедшего через поляризатор р 2, имеем:

| (70) |
Как и в случае фазового модулятора, представим параметр Г (65) в форме (62), (63):

| (71) |
Выразив  через напряжение V, подобно (64), запишем:
через напряжение V, подобно (64), запишем:

| (72) |
где  - полуволновое напряжение.
- полуволновое напряжение.
Амплитудная характеристика ЛМС. Зависимость (70) интенсивности  от разности фаз
от разности фаз  индуцированной внешним полем
индуцированной внешним полем
 (или от напряжения V (72)), называется амплитудной характеристикой АМС. На рис. 13, 14 приведены типичные амплитудные характеристики АМС.
(или от напряжения V (72)), называется амплитудной характеристикой АМС. На рис. 13, 14 приведены типичные амплитудные характеристики АМС.

 Выбор режима работы АМС (напряжения смещения
Выбор режима работы АМС (напряжения смещения  и модулирующего сигнала
и модулирующего сигнала  , как видно из рис.13 (
, как видно из рис.13 ( ) и рис.14 (
) и рис.14 ( ), существенно влияет на свойства переменной составляющей
), существенно влияет на свойства переменной составляющей  ) получаемого на выходе светового луча. В первом случае частота выходного сигнала
) получаемого на выходе светового луча. В первом случае частота выходного сигнала  равна удвоенной частоте входного сигнала
равна удвоенной частоте входного сигнала  , а во втором - частоты обоих сигналов одинаковы.
, а во втором - частоты обоих сигналов одинаковы.
АМС на кристалле ниобата лития. Одним из наиболее распространенных материалов, используемых в качестве рабочего тела АМС, является кристалл ниобата лития (LiNbO3), относящийся к кристаллографическому классу 3т тригональной системы. Символ 3т означает, что группа симметрии кристалла LiNbO3 содержит плоскость симметрии m и лежащую в ней ось симметрии третьего порядка. Число п (порядок оси) определяет, сколько раз фигура совмещается сама с собой при полном повороте вокруг данной оси. Плоскостью симметрии т называется плоскость, которая делит фигуру на две зеркально равные части.
В практических схемах АМС свет направляют вдоль оптической оси, когда 
Вследствие этого обращается в нуль обусловленное естественной анизотропией смещение г0(71) рабочей точки А на кривой (см. рис. 14). Выбрав в качестве т плоскость, проходящую через направление внешнего поля - ось у и оптическую ось - ось z, для параметров  (71) с учетом (58), (59) имеем:
(71) с учетом (58), (59) имеем:

| (73) |
Подставив (73) в (72), для полуволнового напряжения имеем:

Упоминавшаяся в § 23 матрица электрооптических коэффициентов в случае ниобата лития имеет вид:

Литература
Основная
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. - Т. 8: Электродинамика сплошных сред. - М.: Наука, 1992.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. - Т. 2: Теория поля. - М.: Наука, 1988.
Гинзбург В.Л. Теоретическая физика и астрофизика. Дополнительные главы. - М.: Наука, 1975, 1981, 1987.
Сиротин Ю.И., Шаскольская М.П. Основы кристаллофизики. - М.: Наука, 1979.
Корн Г., Корн Т. Справочник по математике: Для научных работников и инженеров. - М.: Наука, 1973.
Фокин А.Г. Макроскопическая проводимость случайнонеоднородных сред. Методы расчета//УФН. - 1996. - Т. 166, № 10.
Дополнительная
Виноградова М.Б., Руденко О.В., Сухорукое А.П. Теория волн. - М.: Наука, 1990.
Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика. - М.: Наука, 1985.
Галицкий В.М., Ермаченко В.М. Макроскопическая электродинамика. - М.: Высшая школа, 1988.
Алексеев А.И. Сборник задач по электродинамике. - М.: Наука, 1977.
11.Батыгин В.В., Топтыгин И.Н. Сборник задач по электродинамике. - М.: Наука, 1970.
Рез И.С., Поплавко Ю.М. Диэлектрики. Основные свойства и применения в электронике. - М.: Радио и связь, 1989.
Волноводная оптоэлектроника / Под ред. Т.Тамира. - М.: Мир, 1991.






