При равновесии механической системы с идеальными связями, виртуальная работа всех активных сил равна нулю.
- Система будет находиться в равновесии.
В положении равновесия все обобщенные силы равны нулю
Теорема: Для того чтобы система материальных точек, подчиненная идеальным стационарным, голономным и удерживающим связям, находилась в равновесии, необходимо и достаточно, чтобы работа всех активных сил на любом виртуальном перемещении системы и скорости всех точек в начальный момент времени равнялись нулю.
15. Интеграл движения: циклические интегралы
f 
(где С - константа)
Интеграл системы уравнений 
(1), или интегралом движения, или первым интегралом, если при подстановке вместо 
решений системы (1), функция f обращается в константу.
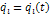
Системы уравнений (1) может иметь не более “2S” – первых интегралов.
Первые интегралы уравнений Лагранжа II-го рода бывают 2-х видов:
1)Обобщенные интегралы энергии.
2)Циклический интеграл.
Циклическая координата – обобщенная координата, которая не входит в функцию Лагранжа, но входит явно в соответствующая ей обобщенная скорость
- циклическая координата
Позиционные координаты – обобщенные координаты, которые явно входят в функцию Лагранжа.
Из (1) для циклической координаты:
- циклическинтеграл
