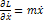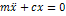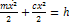Виртуальная работа – работа сил на виртуальных перемещениях системы
Пусть система материальных точек занимает в некоторый момент
времени t какое-то положение. Обозначим через Fk силы, приложенные к точкам системы. Из данного положения при фиксированном времени t, сообщим системе виртуальное перемещение δrk. Будем считать, что на этом перемещении силы Fk, приложенные к системе, не изменяются.
Составим сумму работ этих сил на вирт. перемещении δrk
14. Интеграл движения: обобщенный интеграл движения
f 
(где С - константа)
Интеграл системы уравнений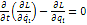 
(1), или интегралом движения, или первым интегралом, если при подстановке вместо 
решений системы (1), функция f обращается в константу.
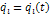
Системы уравнений (1) может иметь не более “2S” – первых интегралов.
Первые интегралы уравнений Лагранжа II-го рода бывают 2-х видов:
1)Обобщенные интегралы энергии.
2)Циклический интеграл.
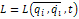
L от времени не зависит
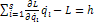(2) - обобщенный интеграл энергии или интеграл Якоби
Допущение: 
- обычный интеграл
Консервативная система – система, которая обладает обычным интегралом энергии.
Из (2) сумма отбрасывается: первый интеграл получается из (2):
