К понятию обобщенные силы приводят преобразование элементарной работы сил и выражают через обобщенные координаты. 
 (1)
(1)
Три способа вычисления обобщенных сил:
1. На основе (1):
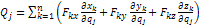

2. Задается 

Множитель Q при изменении обобщенной координаты 
В выражении для виртуальной работы активных сил системы наз. обобщенной силой, соответствующей начальной координате 
3. Для потенциальных сил.



Обобщенная сила в консервативной системе равна частичной производной потенциальной энергии по соответствующей обобщенной координате, взятой с обратным знаком.
Условия равновесия в обобщенных координатах.
Согласно принципу возможных перемещений  .
.
 (2)
(2)

 ,
,  Т.к.
Т.к.  , то
, то  (3)
(3)
Одно вариационное выражение (2) эквивалентно «S» алгебраическим уравнениям (3).
Для равновесия голономных систем необходимо и достаточно, чтобы все вариационные системы были равны нулю.
Частный случай: для потенциальных сил:

11. Устойчивость состояний равновесия: критерий Сильвестра
По Ляпунову: Устойчивое состояние равновесия системы такое, когда при малом начальном отклонении системы все ее точки будут двигаться не уходя от положения равновесия далее наперед заданного расстояния.
Критерий Сильвестра:
Система находится в положении устойчивого равновесия, если квадратичная формула потенциальной энергии этой системы положительна, что возможно в том случае, если все главные диагональные миноры матрицы квадратичной формы и положительны.











