Разложить в ряд Фурье периодический сигнал: sп(n,m) = d(n,m), 0  n
n  4, 0
4, 0  m
m  2
2
(единичные импульсы с периодом: N = 5, M = 3).
Sп(k,l) = 
 d(n,m) exp(-j2pnk/5-j2pml/3) = 1 для всех k и l, т.е. равномерная частотная характеристика в главном диапазоне. Соответственно сам сигнал может быть записан в виде двумерного ряда Фурье:
d(n,m) exp(-j2pnk/5-j2pml/3) = 1 для всех k и l, т.е. равномерная частотная характеристика в главном диапазоне. Соответственно сам сигнал может быть записан в виде двумерного ряда Фурье:
sп(n,m) =(1/20) 
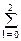 exp(j2pnk/5+j2pml/3).
exp(j2pnk/5+j2pml/3).
Конечные последовательности. Если s(n,m) представляет собой последовательность конечной протяженности, имеющей опорную область RN,M, то периодическую последовательность sп(n,m) с главным периодом RN,M можно сформировать периодическим продолжением s(n,m):
sп(n,m) = 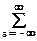
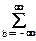 s(n-aN,m-bM),
s(n-aN,m-bM),
s(n, m) = sп(n, m), (n, m) < RN,M.
= 0, в остальных случаях.
Отсюда следует, что любой финитный сигнал может быть полностью определен своим периодическим продолжением и опорной областью.
Аналогично можно записать и для частотной области:
Sп(k, l) = Sa Sb S(k-aN, l-bM).
S(k, l) = Sп(k, l), 0  k
k  N, 0
N, 0  l
l  M
M
= 0, в остальных случаях.
Отсюда значения s(n,m) и S(k,l) можно вычислить с использованием выражений (18.5.1-2) путем последовательности операций:
s(n,m) Þ sп(n,m) Û Sп(k,l) Þ S(k,l).
Практически это означает, что для получения ДПФ последовательности конечной протяженности достаточно из выражений (18.5.1-2) для рядов Фурье убрать знак периодичности, при этом следует помнить, что вычисление отсчетов s(..) вне опорной области приведет к вычислению значений не отсчетов s(..), а отсчетов sп(..) периодического продолжения сигнала s(..).
Таким образом:
1. Дискретизация сигнала в пространственной области вызывает периодизацию частотного спектра сигнала.
2. Дискретизация частотного спектра сигнала вызывает периодизацию его пространственного представления.
3. Прямое и обратное ДПФ сигнала ограниченной протяженности автоматически означает периодизацию как его спектра, так и его пространственного представления.
4. Сигналы, ограниченные в пространстве, можно точно отобразить отсчетами их фурье-преобразования.
5. Частотное представление сигнала с ограниченным спектром обратным фурье-преобразованием может быть точно переведено в пространственную область.
6. Ограниченность как пространственного сигнала, так и его спектра является обязательным условием корректного ДПФ, т.к. в противном случае периодизация сигнала может привести к искажению его спектрального и пространственного представления.
Многомерные последовательности. Определение ДПФ для Р-мерной последовательности с опорной областью R P = { 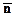 : 0
: 0  ni
ni  Ni-1, i=1,2,3,...,P} производится введением диагональной матрицы значений Ni:
Ni-1, i=1,2,3,...,P} производится введением диагональной матрицы значений Ni:
 =
= 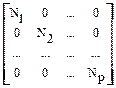 ,
,
при этом P-мерное ДПФ записывается в виде:
S(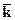 ) =
) =  s(
s(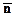 ) exp(-j
) exp(-j 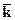 T2p
T2p 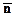 /
/  ). (18.5.3)
). (18.5.3)
s(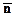 ) =
) = 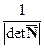
 S(
S(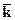 ) exp(j
) exp(j 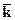 T2p
T2p 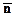 /
/  ). (18.5.4)
). (18.5.4)
Кратко рассмотрим особенности многомерных ДПФ (на примере двумерных последовательностей).
ДПФ суммы двух последовательностей с опорной областью на RN,M равно сумме их ДПФ:
аs(n,m)+bz(n,m) Û aS(k,l)+bZ(k,l),
но при этом все ДПФ должны быть одного размера и этот размер должен быть достаточным, чтобы включить всю опорную область суммарной последовательности аs(n,m)+bz(n,m). Практически это означает, что х(..) и z(..) должны иметь одну и ту же опорную область. Опорная область каждой последовательности при необходимости дополняется нулями.
Операция свертки двух функций в пространственной области отображается операцией умножения фурье-образов функций в частотной области, однако при этом линейная свертка полных пространственных сигналов при ее вычислении через ДПФ в силу периодического продолжения пространственных функций переходит в циклическую свертку (как и для одномерных сигналов). Результат свертки зависит от периодов N и М.
Допустим, что s(n,m) имеет опорную область RP1,P2, a h(n,m) - RQ1,Q2. Результат линейной свертки:
s(n,m) = Sk Sl h(k,l) s(n-k,m-l).
Опорная область последовательности s(n,m):
0  n
n  P1+Q1-1, 0
P1+Q1-1, 0  m
m  P2+Q2-1.
P2+Q2-1.
Следовательно, наложения периодов результата свертки не произойдет и циклическая свертка в главном частотном диапазоне будет равна линейной свертке при опорной области ДПФ:
N  P1+Q1-1, M
P1+Q1-1, M  P2+Q2-1.
P2+Q2-1.






