Прямоугольный растр дискретизации. Из способов обобщения одномерной периодической дискретизации на двумерный случай наиболее простым является периодическая дискретизация в прямоугольных координатах:
s(n,m) = sa(nDx,mDy),
где Dx и Dy - горизонтальный и вертикальный интервалы дискретизации двумерного непрерывного сигнала sa(x,y) с непрерывными координатами x и y. Ниже значения Dx и Dy, как и в одномерном случае, принимаются равными 1.
Дискретизация двумерного, а в общем случае и многомерного сигнала, также приводит к периодизации его спектра и наоборот. Сохраняется также и условие информационной равноценности координатного и частотного представлений дискретного сигнала при равном количестве точек дискретизации в главных диапазонах сигнала. Для прямоугольной дискретизации связь фурье-преобразований непрерывного и дискретного сигналов устанавливается аналогично одномерной дискретизации.
Интегральные преобразования Фурье аналоговых сигналов в непрерывной шкале частот Wx и Wy:
Sa(Wx,Wy) = 
 sa(x,y) exp(-jWxx-jWyy) dxdy. (18.4.1)
sa(x,y) exp(-jWxx-jWyy) dxdy. (18.4.1)
sa(x,y) = 

 Sa(Wx,Wy) exp(jWxx+jWyy) dWxdWy. (18.4.2)
Sa(Wx,Wy) exp(jWxx+jWyy) dWxdWy. (18.4.2)
Дискретные преобразования Фурье:
S(k,l) = 
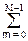 s(n,m) exp(-jn2pk/N-jm2pl/M), (18.4.3)
s(n,m) exp(-jn2pk/N-jm2pl/M), (18.4.3)
S(k,l) =  exp(-jn2pk/N)
exp(-jn2pk/N) 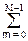 s(n,m) exp(-jm2pl/M), (18.4.3')
s(n,m) exp(-jm2pl/M), (18.4.3')
s(n,m) = 

 S(k,l) exp(-jn2pk/N-jm2pl/M). (18.4.4)
S(k,l) exp(-jn2pk/N-jm2pl/M). (18.4.4)
s(n,m) = 
 exp(-jn2pk/N)
exp(-jn2pk/N)  S(k,l) exp(-jm2pl/M). (18.4.4')
S(k,l) exp(-jm2pl/M). (18.4.4')
Выражения (18.4.3') и (18.4.4') показывают, что двумерное ДПФ по прямоугольному растру дискретизации данных может вычисляться с помощью одномерных последовательных ДПФ. Вторые суммы выражений являются одномерными ДПФ сечений функций s(n,m) и S(k,l) по линиям n и k соответственно, а первые - одномерными ДПФ вычисленных функций в сечениях по m и l. Другими словами, исходные матрицы значений s(n,m) и S(k,l) пересчитываются сначала в промежуточные матрицы с ДПФ по строкам (или по столбцам), а промежуточные - в окончательные с ДПФ по столбцам (или соответственно по строкам).
Интерполяционный ряд восстановления двумерного сигнала. Если непрерывный сигнал sa(x,y) является сигналом с ограниченным спектром, а периоды дискретизации выбраны достаточно малыми и спектры соседних периодов не перекрываются:
Sa(Wx,Wy) = 0 при |Wx|  p/Dx, |Wy|
p/Dx, |Wy|  p/Dx,
p/Dx,
то, как и в одномерном случае, сигнал sa(x,y) может быть восстановлен по дискретному сигналу с использованием двумерного аналога ряда Котельникова-Шеннона:
sa(x,y) = Sn Sm s(n,m)  . (18.4.5)
. (18.4.5)
Сигнал с неограниченным спектром также может быть дискретизирован, однако в этом случае имеет место наложение спектров в смежных периодах, при этом высокие частоты, большие частоты Найквиста, будут "маскироваться", как и в одномерном случае, под низкие частоты главного периода. Эффект "отражения" от границ периода дает еще более сложную картину вследствие интерференции частот, отраженных по разным координатам.
 Рис. 18.4.1.
Рис. 18.4.1.
|
Произвольный растр дискретизации. Понятие прямоугольной дискретизации обобщается на произвольный растр дискретизации с линейно независимыми векторами v1 = (v11,v21)T и v2 = (v12,v22)T, где T - индекс транспонирования (рис. 18.4.1). Координаты двумерного периодического множества отсчетов на плоскости (x,y):
x = v11n + v12m,
y = v21n + v22m.
С использованием векторных обозначений:
 =
= 

где  = (x,y)T,
= (x,y)T,  =(n,m)T,
=(n,m)T,  =(v1 | v2)- матрица дискретизации. Определитель матрицы
=(v1 | v2)- матрица дискретизации. Определитель матрицы  не равен нулю, если вектора v1 и v2 линейно независимы. При дискретизации непрерывного сигнала sa(x,y) матрицей
не равен нулю, если вектора v1 и v2 линейно независимы. При дискретизации непрерывного сигнала sa(x,y) матрицей  формируется дискретный сигнал:
формируется дискретный сигнал:
s( ) Ü sa(
) Ü sa(
 ).
).
Двумерное интегральное преобразование Фурье непрерывного сигнала по непрерывному вектору  = (W1,W2)T:
= (W1,W2)T:
Sa( ) =
) =  sa(
sa( ) exp(-j
) exp(-j  T
T  ) d
) d  , (18.4.6)
, (18.4.6)
sa( ) =
) = 
 Sa(
Sa( ) exp(j
) exp(j  T
T  ) d
) d  , (18.4.7)
, (18.4.7)
Данные интегралы являются двойными, поскольку дифференциалы d  и d
и d  являются векторами.
являются векторами.
Преобразование Фурье дискретного сигнала:
S(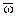 ) = Sn s(
) = Sn s( ) exp(-j
) exp(-j 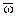 T
T  ), (18.4.8)
), (18.4.8)
s( ) =
) = 
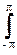 S(
S(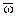 ) exp(j
) exp(j 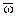 T
T  ) d
) d 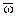 . (18.4.9)
. (18.4.9)
где: 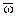 = (wх,wу)T .
= (wх,wу)T .
Выражение s( ) может быть получено дискретизацией выражения sa(
) может быть получено дискретизацией выражения sa( ) (18.4.7):
) (18.4.7):
s( ) = sa(
) = sa(
 ) =
) = 
 Sa(
Sa( ) exp(j
) exp(j  T
T 
 ) d
) d  .
.
После подстановки в это выражение значения 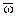 =
= 
 T, получаем:
T, получаем:
s( ) =
) = 

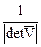 Sa(
Sa(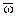 /
/  T) exp(j
T) exp(j 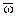 Т
Т  ) d
) d 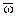 .
.
Или, с учетом периодичности по квадратным областям плоскости 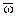 :
:
s( ) =
) = 
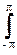
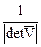
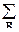 Sa((
Sa(( -2p
-2p  )/
)/  T) exp(j
T) exp(j  Т
Т  ) d
) d 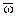 , (18.4.10)
, (18.4.10)
где  - вектор целочисленных значений периодов дискретизированной функции по осям wх и wу. Сравнивая последнее выражение с выражением (18.4.9), получаем:
- вектор целочисленных значений периодов дискретизированной функции по осям wх и wу. Сравнивая последнее выражение с выражением (18.4.9), получаем:
S(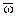 ) =
) = 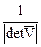
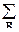 Sa((
Sa((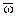 -2p
-2p  )/
)/  T),
T),
S(
 T) =
T) = 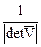
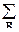 Sa(
Sa( -
- 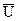
 ), (18.4.11)
), (18.4.11)
где 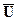 - матрица периодичности:
- матрица периодичности:
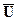 Т
Т  = 2p
= 2p  , (18.4.12)
, (18.4.12)
которой задаются два линейно независимых вектора периодичности спектра,  - единичная матрица 2 х 2. Выражение (18.4.11) определяет связь между преобразованиями Фурье дискретных и аналоговых сигналов.
- единичная матрица 2 х 2. Выражение (18.4.11) определяет связь между преобразованиями Фурье дискретных и аналоговых сигналов.
 Рис. 18.4.2.
Рис. 18.4.2.
|
Как и в одномерном случае, интервалы дискретизации Dx и Dy определяют главный период двумерного спектра соответственно по осям wx и wy и частоты Найквиста: wxN = p/Dx и wyN = p/Dy. Спектр дискретного сигнала также является периодическим продолжением спектра аналогового сигнала. Для исключения искажений спектра (наложения спектров боковых периодов на главный период) предельные частоты сигнала должны быть меньше частот Найквиста. На рис. 18.4.2 приведен пример центральной части спектра дискретного сигнала при Dx=1 и Dy=1.
В случае прямоугольной дискретизации:
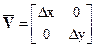 , det
, det  = DхDу, (18.4.13)
= DхDу, (18.4.13)
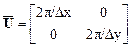 . (18.4.14)
. (18.4.14)
Интерполяция дискретных сигналов. Для сигнала с ограниченным спектром изменением матрицы дискретизации  можно подобрать матрицу периодичности
можно подобрать матрицу периодичности 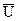 таким образом, чтобы в правой части выражения (18.4.11) не было перекрытия спектров. Тогда для значений по точкам
таким образом, чтобы в правой части выражения (18.4.11) не было перекрытия спектров. Тогда для значений по точкам 
 T области С главного периода спектра выражение (18.4.11) упрощается:
T области С главного периода спектра выражение (18.4.11) упрощается:
S(
 T) = Sa(
T) = Sa( ) / |det
) / |det  |. (18.4.15)
|. (18.4.15)
Sa( ) = |det
) = |det  | S(
| S(
 T) = |det
T) = |det  | S(
| S(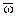 ),
),  Î С. (18.4.16)
Î С. (18.4.16)
Из выражения (18.4.16) следует, что при корректной дискретизации непрерывной двумерной функции ее спектр с точностью до нормировочного множителя |det  | может быть восстановлен по спектру дискретной функции. Соответственно, выполнив обратное преобразование Фурье левой и правой части равенства (18.4.16), получим уравнение восстановления непрерывной функции по ее дискретному варианту (многомерный аналог интерполяционного ряда Котельникова-Шеннона):
| может быть восстановлен по спектру дискретной функции. Соответственно, выполнив обратное преобразование Фурье левой и правой части равенства (18.4.16), получим уравнение восстановления непрерывной функции по ее дискретному варианту (многомерный аналог интерполяционного ряда Котельникова-Шеннона):
sa( ) =
) = 
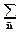 s(
s(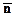 )
)  exp(j
exp(j  T (
T ( -
- 
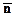 )) d
)) d  .
.
sa( ) =
) = 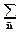 s(
s(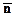 ) f(
) f( -
- 
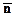 ), (18.4.17)
), (18.4.17)
где f(..) – интерполяционная функция:
f( -
- 
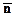 ) =
) = 
 exp(j
exp(j  T (
T ( -
- 
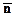 )) d
)) d  . (18.4.18)
. (18.4.18)
Все приведенные векторные уравнения могут быть обобщены на Р-мерные функции с заменой константы 4p2 там, где она встречается, на (2p)P.
Прямоугольный и гексагональный растры дискретизации. В принципе, сигнал с ограниченным спектром можно представить по различным растрам дискретизации. Выбор растра обычно производят из условия минимальной плотности отсчетов на плоскости, т.е. минимизацией величины |det  |, при котором обеспечивается отсутствие наложений для частот анализируемых сигналов.
|, при котором обеспечивается отсутствие наложений для частот анализируемых сигналов.
На практике для двумерных сигналов используют, как правило, только два варианта растров дискретизации - прямоугольный и гексагональный. Прямоугольному варианту соответствуют диагональные матрицы дискретизации и периодичности (18.4.13-14). Для гексагональной дискретизации, пример которой приведен на рис. 18.4.1, в частном случае при Dt = Dх  каждый отсчет располагается на равном расстоянии от шести ближайших отсчетов, при этом матрицы дискретизации:
каждый отсчет располагается на равном расстоянии от шести ближайших отсчетов, при этом матрицы дискретизации:
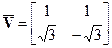 ,
,  .
.
Допустим, имеем сигнал с частотным спектром, ограниченным круговой областью частот wr:
Sa(wх,wу) = 0 при wх2+wу2 > wr2.
Круговая область частот вписывается без перекрытий в квадрат со стороной 2wr или в шестиугольник со стороной 2wr/  . Матрицы дискретизации:
. Матрицы дискретизации:
 пр =
пр = 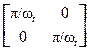 , det
, det  = p2/wr2,
= p2/wr2,
 гекс =
гекс =  , det
, det  = 2p2/(wr2
= 2p2/(wr2  ).
).
Поскольку плотность отсчетов пропорциональна 1/|det  |, то отсюда следует, что для представления одного и того же сигнала гексагональный растр дискретизации требует на 13.4% меньше отсчетов по сравнению с прямоугольным. Эффективность "гексагональной" матрицы возрастает при увеличении размерности сигнала. Так, при 4-мерном сигнале для "гексагональной" матрицы требуется в 2 раза меньше отсчетов, чем для "прямоугольной".
|, то отсюда следует, что для представления одного и того же сигнала гексагональный растр дискретизации требует на 13.4% меньше отсчетов по сравнению с прямоугольным. Эффективность "гексагональной" матрицы возрастает при увеличении размерности сигнала. Так, при 4-мерном сигнале для "гексагональной" матрицы требуется в 2 раза меньше отсчетов, чем для "прямоугольной".






