Пример расчета неразделимого импульсного отклика

Определить импульсный отклик идеального кругового фильтра нижних частот:

H(w_x,w_y) = 1 при w_x²+w_y² <R²<p²; H(w_x,w_y) = 0 в остальных случаях.

Вычисления по круговой области целесообразно выполнять в полярных координатах: w = ,

j = arctg(w_y/w_x), f = arctg(m/n), при этом выражение 18.3.2 перепишется в следующем виде:

h(n,m) = w exp[jw cos(f-j)] dj dw =

= w J_o(w ) dw = J₁(R ) / ,

где J_o(…), J₁(…)- функции Бесселя 1-го рода 0-го и 1-го порядков соответственно.

На рис. 18.3.2 приведена пространственная форма импульсного отклика фильтра, расчет которой проведен при R = 1 с ограничением по N = 10 и M = 10, и сечения отклика по координате m.

Рис. 18.3.2. Круговой низкочастотный фильтр (справа - сечения по координате m).

Свойства двумерного преобразования Фурье. Вышеприведенные преобразования импульсного отклика в частотный отклик и наоборот представляют собой двумерные дискретные преобразования Фурье с прямоугольным растром дискретизации информации, эквивалентные одномерным преобразованиям. На двумерные преобразования с прямоугольным растром переносятся и другие свойства одномерных систем. В частности:

1. Фурье-преобразования сигналов.

S(w_x,w_y) = S_n S_m s(n,m) exp(-jnw_x-jmw_y). (18.3.3)

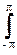
s(n,m) = 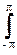S(w_x,w_y) exp(jnw_x+jmw_y) dw_xdw_y. (18.3.4)

2. Теорема о свертке.

z(n,m) = h(n,m) _** s(n,m) Û H(w_x,w_y) S(w_x,w_y) = Z(w_x,w_y).

z(n,m) = c(n,m) s(n,m) Û C(w_x,w_y) _** S(w_x,w_y) = Z(w_x,w_y).

3. Основные свойства Фурье-преобразования.

1) Линейность (в том числе для любых комплексных чисел a и b):

а×s(n,m)+b×z(n,m) Û aS(w_x,w_y)+bZ(w_x,w_y).

2) Пространственный сдвиг:

s(n-N,m-M) Û S(w_x,w_y) exp(-jNw_x-jMw_y).

3) Дифференцирование:

dS(w_x,w_y)/dw_x Û -jn s(n,m),

dS(w_x,w_y)/dw_y Û -jm s(n,m),

d²S(w_x,w_y)/(dw_x dw_y) Û -nm s(n,m).

4) Комплексное сопряжение:

х*(n,m) Û S*(-w_x,-w_y).

Вещественная и мнимая части Фурье-образов последовательностей s(n,m):

S(w_x,w_y) = S*(-w_x,-w_y).

Re [S(w_x,w_y)] = Re [S(-w_x,-w_y)].

Im [S(w_x,w_y)] = -Im [S(-w_x,-w_y)].

5) Теорема Парсеваля:

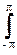
S_n S_m s(n,m) s*(n,m) = 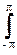S(w_x,w_y) S*(w_x,w_y) dw_x dw_y.

В частности, при s(n,m) = s(n,m):

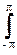
S_n S_m |s(n,m)|² = 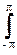|S(w_x,w_y)|² dw_x dw_y,

где левая часть уравнения представляет собой полную энергию дискретного сигнала s(n,m), a функция |S(w_n,w_m)|² - спектральную плотность энергии сигнала.