Пример расчета частотного отклика системы

Определить частотную характеристику системы с импульсным откликом:

h(0,0) = 0.25, h(0, 1) = 0.125, h( 1,0) = 0.125, h( 1, 1) = 0.0625.

Частотный отклик:

H(w_x,w_y) = 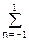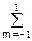h(n,m)exp(-jnw_x-jmw_y) = 0.25+0.125[exp(-jw_x)+exp(jw_x)+exp(-w_y)+exp(jw_y)]+

+0.0625[exp(-jw_x-jw_y)+exp(-jw_x+jw_y)+exp(jw_x-jw_y)+exp(jw_x+jw_y)] = 0.25(1+cos w_x)(1+cos w_y).

Система является примером двумерного фильтра нижних частот. Частотный отклик системы на плоскости (w_x,w_y), приведенный на рис. 18.3.1, имеет осевую симметрию с коэффициентом передачи 1 в центре (w_x=0, w_y=0) со спадом до нуля при w_x= p и w_y= p.

Рис. 18.3.1. Частотная характеристика ФНЧ.

При разделимости импульсного отклика частотный отклик многомерных систем также является разделимой функцией:

h(k,l)= q(k)g(l) Û Q(w_x)G(w_y)= H(w_x,w_y)

Q(w_x) = S_k q(k) exp(-jk×w_x). G(w_y) = S_l g(l) exp(-jl×w_y).

Импульсный отклик системы. Выражение (18.3.1), по существу, описывает разложение функции Н(w_x,w_y) в двумерный рад Фурье с коэффициентами разложения в виде отсчетов импульсного отклика h(k,l), т.е. прямое преобразование Фурье. Очевидно, что обратным преобразованием Фурье с интегрированием в пределах одного периода из частотного отклика H(w_x,w_y) можно получить импульсный отклик системы:

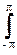
h(k,l) = 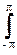H(w_x,w_y) exp(jkw_x+jlw_y) dw_xdw_y. (18.3.2)