Системы осуществляют преобразование сигналов. Формализованная система - это оператор (операция) отображения входного сигнала на выходной: z(x,y) = Т[s(x,y)].
Базовыми операциями в системах, комбинациями которых осуществляются преобразования, являются операции скалярного умножения, сдвига и сложения:
z(n,m) = c s(n,m),
z(n,m) = s(n-N,m-M),
z(n,m) = s(n,m)+u(n,m).
Используя базовые операции, любую двумерную последовательность можно разложить на сумму взвешенных двумерных единичных импульсов:
s(n,m) = 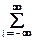
 s(i,j) d(n-i,m-j). (18.2.1)
s(i,j) d(n-i,m-j). (18.2.1)
Обобщением скалярного умножения является пространственное маскирование:
z(n,m) = cn,m s(n,m). (18.2.2)
Правая часть равенства (18.2.2) представляет собой поэлементное произведение входного сигнала на совокупность чисел сn,m.
Кроме линейных операций в системах используются также безынерционные нелинейные преобразования с независимым нелинейным воздействием на значения отсчетов входной последовательности. Пример операции - возведение в квадрат:
zn,m = (sn,m)2.
Линейные системы. Система считается линейной при выполнении двух условий:
1. Пропорциональное изменение входного сигнала вызывает пропорциональное изменение выходного сигнала.
2. Суммарный сигнал двух входных последовательностей дает суммарный сигнал двух соответствующих выходных последовательностей.
Другими словами, если оператор Т[s(x,y)] описывает линейную систему и имеет место z(x,y) = Т[s(x,y)], q(x,y) = Т[u(x,y)], то Т[as(x,y)+bu(x,y)] = az(x,y)+bq(x,y). Линейные системы подчиняются принципу суперпозиции сигналов.
В выражении (18.2.1) значения s(i,j) можно рассматривать как скалярные множители для соответствующих единичных импульсов. Применяя оператор преобразования Т[.] к левой и правой части (18.2.1), получаем:
Т[s(n,m)] = у(n,m) = 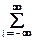
 s(i,j) T[d(n-i,m-j)],
s(i,j) T[d(n-i,m-j)],
z(n,m) = 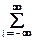
 s(i,j) hij(n,m), (18.2.3)
s(i,j) hij(n,m), (18.2.3)
где hij(n,m) - отклик системы в точке (n,m) на единичный импульс в точке (i,j). Если импульсный отклик hij(n,m) определен для всех точек (i,j), то отклик системы на произвольный многомерный сигнал, как и для одномерных систем, находится с помощью суперпозиции.
Инвариантность к сдвигу. Система инвариантна к сдвигу, если сдвиг входной последовательности приводит к такому же сдвигу выходной последовательности:
Т[s(n-N,m-M)] = z(n-N,m-M).
Линейность и инвариантность к сдвигу являются независимыми свойствами системы. Так, пространственное маскирование линейно, но не инвариантно к сдвигу, а безынерционные операторы нелинейны, но инвариантны к сдвигу.
В дальнейшем ограничимся рассмотрением только систем, широко распространенных при решении практических задач - линейных и инвариантных к сдвигу (ЛИС-системы).
Импульсный отклик на произвольно расположенный входной импульс, как следует из выражения (18.2.3), описывается выражением:
hij(n,m) = T[d(n-ni,m-mj)].
Для частного случая i = j = 0 имеем:
ho(n,m) = T[d(n,m)].
Используя принцип инвариантности к сдвигу, получим:
hij(n,m) = ho(n-i,m-j) = h(n-i,m-j), (18.2.4)
т.e. импульсный отклик на произвольно расположенный входной импульс равен сдвинутому импульсному отклику на входной импульс, расположенный в начале координат.
Двумерная свертка. Подставляя (18.2.4) в выражение (18.2.3), получаем:
z(n,m) = Si Sj s(i,j) h(n-i,m-j). (18.2.5)
Двумерная дискретная свертка (18.2.5), является аналогом одномерной дискретной свертки. При замене переменных n-i = k, m-j = l, получим:
z(n,m) = Sk Sl h(k,l) s(n-k,m-l), (18.2.5')
т.е. двумерная свертка коммутативна, как и одномерная. В такой же мере она обладает свойством ассоциативности по отношению к последовательности операций свертки нескольких функций (результат не зависит от порядка свертки) и свойством дистрибутивности по отношению к операции свертки с суммой функций (результат аналогичен сумме сверток с каждой функцией). Эти свойства определяют и основное свойство двумерных (и многомерных) линейных систем при их параллельном и/или последовательном соединении – результирующая система также является линейной.
Для упрощения символьного аппарата двумерную свертку обозначают индексом (**):
z(n,m) = h(k,l) ** s(n-k,m-l).
При обобщении этого выражения на многомерные системы, в векторной форме:
z( )= h(
)= h( ) ** s(
) ** s( -
-  ).
).
Разделимые системы. Если импульсный отклик системы может быть разделен:
h(k,l) = h(k) h(l), (18.2.6)
то выражение (18.2.5') принимает вид:
z(n,m) = Sk h(k) Sl h(l) s(n-k,m-l), (18.2.7)
или: z(n,m) = Sk h(k) g(n-k,m), g(n-k,m) = Sl h(l) s(n,m-l).
Массив g(n,m) вычисляется одномерной сверткой столбцов массива s(n,m) при n = const (сечения массива по координатам n) с откликом h(l), с последующим вычислением выходного массива z(n,m) одномерной сверткой строк g(n,m) при m = const с откликом h(k). Результат не изменится, если сначала выполнять свертку по строкам, а затем по столбцам. Система с откликом вида (18.2.6) называется разделимой. Отметим, что в разделимой системе входной и выходной сигнал не обязаны быть разделимыми.
Аналогичные разделимые системы могут существовать и в многомерном варианте.
Устойчивость системы. Интерес для практики представляют только устойчивые системы, обеспечивающие определенный конечный результат системной операции на конечные входные сигналы. Необходимым и достаточным условием устойчивости системы является абсолютная суммируемость ее импульсного отклика: Sk Sl |h(k,l)| < 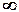 .
.
Специальные двумерные системы. На практике используются также системы с несколькими входами и/или выходами.
Допустим, система имеет i-входы и j-выходы, линейна и инвариантна к сдвигу по переменной t. Если на i-вход системы поступает одномерный единичный импульс di(t) при нулевых сигналах на остальных входах, то j-выходные сигналы будут импульсным откликом системы hij(t). При известном полном ансамбле значений hij для всех i-входов, для произвольной комбинации входных сигналов si(t) сигнал на j-выходе будет определяться выражением:
zj(t) = Si Sk hij(k) si(t-k). (18.2.8)






