Частотный отклик системы. Допустим, что двумерная ЛИС-система имеет импульсный отклик h(kDx,lDy). Подадим на вход системы сигнал вида комплексной синусоиды:
s(n,m) = exp(jnDx×wx+jmDy×wy),
где wx и wy – значения частоты сигнала соответственно по координатам x и y. Принимая Dx = 1, Dy = 1 и выполняя двумерную свертку (18.2.5), получаем:
z(n,m) =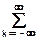 
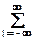h(k,l) exp[j×wx×(n-k)+j×wy×(m-l)] =
= exp(jn×wx+jm×wy) 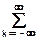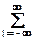h(k,l) exp(-jk×wx-jl×wy) = H(wx,wy) exp(jn×wx+jm×wy).
H(wx,wy) = 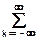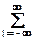h(k,l) exp(-jk×wx-jl×wy). (18.3.1)
Таким образом, выходной сигнал представляет собой комплексную синусоиду с теми же значениями частоты, что и у входного сигнала, с изменением амплитуды и фазы за счет комплексного множителя H(wx,wy), который носит название частотного отклика (частотной характеристики) системы. Для дискретных сигналов частотный отклик периодичен с периодом 2p по обеим частотным переменным:
H(wx+2pk,wy+2pl) = H(wx,wy).
