Двумерные и многомерные сигналы [9]

Рис. 18.1.1.

Понятие многомерного сигнала. Многомерные сигналы представляют собой функции P независимых переменных при P>1. В общем случае, сигнал может быть непрерывным, дискретным или смешанным. Понятия непрерывности и дискретности аналогичны одномерным сигналам. Что касается смешанного сигнала, то это многомерный сигнал, который описывается функцией некоторого количества непрерывных и некоторого количества дискретных переменных. Пример смешанного двумерного сигнала: ансамбль непрерывных сигналов, изменяющихся во времени (t - вторая переменная), снимаемых с набора сейсмических приемников сейсмотрассы (номера датчиков - первая переменная).

В общем случае, двумерный непрерывный сигнал представляет собой функцию, значения которой зависят от двух независимых переменных (аргументов, координат):

s(x,y) = sin(x²+y²), - 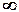< x,y < 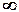(18.1.1)

График функции (в пределах одного периода) приведен на рис. 18.1.1.

Двумерный дискретный сигнал (цифровой массив) - это функция, определенная на совокупности пар числовых значений координат с определенным шагом дискретизации Dx и Dy. В общем случае, при различной физической размерности аргументов x и y, значения Dx и Dy не равны друг другу:

s_n,m = s(nDx,mDy), - 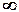< n,m < 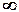. (18.1.1')

Элемент последовательности s_n,m представляет собой отсчет двумерной функции s в координатной точке (x=nDx,y=mDy), где значения x и y – независимые переменные (аргументы) функции. Для числовых массивов значения шага дискретизации по аргументам также могут приниматься равными 1 (независимо от размерности) и использоваться аргументация s(n,m) º s_n,m. Результаты геофизических съемок какого-либо одного геофизического параметра по поверхности земли относятся к двумерным функциям: дискретным - если это отсчеты в отдельных точках по определенной координатной сети (x,y), или смешанным - если это непрерывная регистрация данных по профилям (например - мощности экспозиционной дозы гамма излучения горных пород при аэросъемке). Но в настоящее время геофизические съемки относятся даже не к двумерным, а к многомерным функциям, так как регистрируется, как правило, сразу несколько физических параметров геологических сред. Так, например, при спектрометрической съемке естественной радиоактивности горных пород регистрируется содержание в горных породах урана, тория и калия, в гравиразведке - трехкоординатный вектор силы тяжести, и т.п. Если на какой-либо площади проведена съемка нескольких видов геофизики, то их результаты также могут рассматриваться в совокупности, как многомерная функция физических параметров данной геологической среды.

По определениям (18.1.1) двумерные функции и сигналы, равно как и многомерные, имеют бесконечную протяженность по координатам. На практике мы всегда имеем дело с конечными координатами наших данных. Учитывая это, будем считать, что значения наших сигналов за пределами определенных координат равны нулю.

Отметим некоторые двумерные последовательности (функции, сигналы), имеющие специальные названия.

Рис. 18.1.2.

Двумерный единичный импульс d(nDx,mDy) = d_n,m или единичный отсчет:

d_n,m = 1, при n = m = 0.

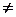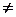= 0, при n 0, m 0.

d_n,m = d_n d_m,

где d_n, d_m - одномерные единичные импульсы (импульсы Кронекера) по координатам n и m. Стилизованное графическое представление двумерного единичного импульса приведено на рис. 18.1.2.

Произвольное расположение двумерного единичного импульса по координатам n₁, m₁ соответственно записывается в виде: d((n-n₁)Dx,(m-m₁)Dy) = d_n-n1,m-m1. Попутно напомним, что математическая запись импульса Кронекера обозначает не единичный отсчет, а функцию, определяющую место положения единичного отсчета и нулевые значения по остальным координатам (аргументам).

Рис. 18.1.3.

Двумерный линейный импульс представляет собой последовательность единичных отсчетов по одной координате: s(n,m) = d(n) или s(n,m) = d(m).

На рис. 18.1.3 приведены два двумерных линейных импульса, первый - по координате m = 0: s(n,m) = d(m), и второй импульс по координате n = 2: s(n,m) = d(n-2).

Очевидно, что для P-мерных случаев точно таким же образом могут быть определены P-мерные единичные импульсы, P-мерные линейные импульсы, P-мерные площадные импульсы и т.д., хотя понятие импульса, заимствованное из теории одномерных сигналов, здесь несколько не к месту.

Рис. 18.1.4.

Двумерная единичная ступенька u(n,m), представленная на рис. 18.1.4, определяется выражением:

u(n,m) = 1, при n 0 и m 0,

= 0, в остальных случаях.

u(n,m) = u(n) u(m),

где u(j) представляют собой единичные ступеньки соответственно по координатам n и m: u(j)=1 при j 0, u(j)=0 при j<0. Двумерная единичная ступенька отлична от нуля в одном квадранте (n,m)- плоскости.

Экспоненциальная последовательность: s(n,m) = aⁿb^m, - 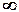< n,m < 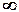, где а и b в общем случае комплексные числа. При а = exp(jw₁), b = exp(jw₂), |а|=1, |b|=1:

s(n,m) = exp(jnw₁+jmw₂) = cos(nw₁+mw₂)+jsin(nw₁+mw₂).

Экспоненциальные последовательности, как и в одномерном случае, являются собственными функциями двумерных линейных систем, инвариантных к сдвигу.

Разделимые последовательности. Разделимой называют последовательность, которую можно представить в виде произведения одномерных последовательностей. Так, для двумерной разделимой последовательности:

s(n,m) = s(n) s(m).

Разделение возможно для немногих практических сигналов. Однако любое двумерное множество с конечным числом ненулевых отсчетов разлагается на конечную сумму разделимых последовательностей:

s(n,m) = s_i×n(n) s_i×m(m),

где N- число ненулевых строк или столбцов массива. В крайнем случае, для этого достаточно выразить s(n,m) в виде суммы отдельных строк:

s(n,m) = s(n,i) d(m-i). (18.1.2)

Рис. 18.1.5.

Конечные последовательности. Важным классом сигналов являются последовательности конечной протяженности, для которых сигнал равен нулю вне определенной области, называемой опорной областью сигнала. На рис.18.1.5 условно представлена двумерная последовательность конечной протяженности, значения которой отличны от нулевых только внутри ограниченной прямоугольной области -3 n 2, -2 m . Опорная область сигнала может быть произвольной формы и выходить за пределы сигнала, частично включая нулевые отсчеты. Отсчеты за пределами опорной области считаются равными нулю.

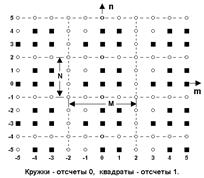Рис. 18.1.6.

Периодические последовательности. Двумерные последовательности могут быть периодическими, регулярно повторяющимися в пространстве. Последовательность, удовлетворяющая условиям:

s(n,m+M) = s(n,m),

s(n+N,m) = s(n,m), (18.1.3)

обладает периодичностью в двух направлениях, по n и по m. Значения М и N называют интервалами периодичности сигнала соответственно по координатам m и n (горизонтальными и вертикальными интервалами периодичности). Прямоугольная форма области периода (пример на рис.18.1.6) наиболее удобна при обработке данных, но не является единственно возможной.

Для двумерных последовательностей условия (18.1.3) могут рассматриваться как частный случай общих условий периодичности:

s(n+N₁, m+M₁) = s(n,m), (18.1.4)

s(n+N₂, m+M₂) = s(n,m),

D = N₁M₂ - N₂M₁ 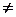0.

Рис. 18.1.7.

Упорядоченные пары (N₁,M₁) и (N₂,M₂) представляют собой смещения от отсчетов одного периода к соответствующим отсчетам других периодов и могут рассматриваться как векторы N и M, которые образуют области периодов в форме параллелограмма. Линейная независимость векторов обеспечивается при ненулевом определителе D, а количество отсчетов в пределах периода равно |D|. Пример периодической последовательности с векторами (4,4) и (3,-5) приведен на рис. 18.1.7.

Понятие периодичности можно обобщить на многомерные сигналы. P-мерный сигнал s() будет представлять собой P-мерную периодическую последовательность, если существует P линейно независимых P-мерных целочисленных N -векторов периодичности, с которыми выполняется условие:

s() = s( + ), i = 1,2,3,...,P.

Столбцы векторов N _i образуют матрицу периодичности N размером P х P. Векторы периодичности матрицы линейно независимы при наличии у матрицы ненулевого определителя. Абсолютное значение определителя равно числу отсчетов в периоде. Последовательность s() прямоугольно периодична для случаев диагональной матрицы N. Если функция s() периодична с матрицей периодичности N, то для любого целочисленного вектора Р имеет место s( + ) = s(), и матрица PN также будет матрицей периодичности для s(). Отсюда следует, что любая многомерная периодическая последовательность имеет не единственную матрицу периодичности.