В том случае, когда источниковый член S зависит от Т, можно выразить эту зависимость в линейной форме с помощью уравнения 
. Это делается по той причине, что, во-первых, номинально линейная система допускает только формально линейную зависимость, и, во-вторых, введение линейной зависимости лучше, чем предположение о постоянстве S.
Если S является нелинейной функцией Т, то функцию надо линеаризовать, т.е. определить значения SC и SP, которые сами могут зависеть от Т. В процессе каждого итерационного цикла SC и SP пересчитывают с учетом новых значений Т.
Линеаризующая зависимость для S должна быть хорошим представлением зависимости S от T. В дальнейшем будем следовать основному правилу относительно неположительности SP.
Существует много различных способов разложения заданного выражения для S на SC и SPTP. Некоторые из них проиллюстрированы ниже. Символ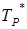 
* используется для обозначения начального значения или значения ТР на нулевой итерации.
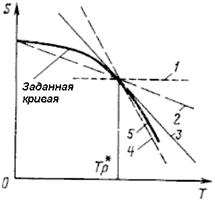
Пример. Дано: 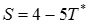 . Некоторые возможные линеаризации этой функции (5) показаны на рисунке.
1. 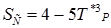 ,  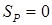. Такое приближение (1)для тех, кто не в состоянии воспользоваться преимуществами известной зависимости S от Т.
2.  ,  . Это разложение (2) выглядит как корректная линеаризация, но заданная зависимость S от Т более крутая, чем та, которую дает приближение.
| 
|
3. Рекомендуемый способ найти касательную к кривой, т.е.:
Таким образом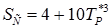 
, 
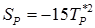. Такая линеаризация (3) дает касательную к кривой S от Т в точке .
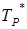4. 
, 
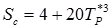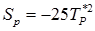. Эта линеаризация (4), дающая более крутую зависимость, чем заданная зависимость S от Т, приведет к замедлению сходимости.
На схеме, представленной на рисунке, прямые линии с положительным тангенсом угла наклона будут нарушать правило 3. Среди прямых с отрицательным тангенсом угла наклона линия, касательная к заданной кривой, является лучшим вариантом. Более крутые линии можно использовать, но это обычно приводит к более медленной сходимости. Менее крутые линии неудобны, так как они не обеспечивают заданной скорости уменьшения S в зависимости от Т.
