Краткое рассмотрение некоторых дифференциальных уравнений, описывающих теплообмен и гидродинамику, показывает, что интересующие нас зависимые переменные подчиняются обобщенному закону сохранения. Если обозначить зависимую переменную Ф, то обобщенное дифференциальное уравнение примет вид
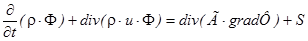
где Г — коэффициент диффузии; S — источниковый член.
Конкретный вид Г и S зависит от смысла переменной Ф (в действительности следовало бы использовать обозначения ГФ и SФ, но это привело бы к слишком большому количеству нижних индексов в дальнейших выкладках).
В обобщенное дифференциальное уравнение входят четыре члена: нестационарный, конвективный, диффузионный и источниковый. Зависимая переменная Ф обозначает различные величины, такие, как массовая концентрация химической компоненты, энтальпия или температура, составляющая скорости, кинетическая энергия турбулентности или масштаб турбулентности. При этом коэффициенту диффузии Г и источниковому члену S следует придать соответствующий каждой из этих переменных смысл.
Не все диффузионные потоки определяются градиентом соответствующей переменной. Однако запись диффузионного члена уравнения в виде 
не ограничивает применение обобщенного уравнения для Ф случаями, когда диффузионные процессы обусловлены соответствующими градиентами. Ту часть диффузионного члена уравнения, которую нельзя выразить в указанном виде, всегда можно записать как часть источникового члена; фактически коэффициент диффузии Г можно даже считать равным нулю.
Явная запись диффузионного члена в обобщенном уравнении для Ф через ее градиент использовалась потому, что для большинства зависимых переменных диффузионный член имеет именно такой вид.
Входящая в уравнение плотность может быть связана с такими переменными, как массовая концентрация и температура, через уравнение состояния. Эти переменные и составляющие скорости также подчиняются обобщенному дифференциальному уравнению. Кроме того, поле скорости должно удовлетворять дополнительному ограничению, а именно закону сохранения массы или уравнению неразрывности.
Обобщенное уравнение записано в векторном виде. Однако, можно представить также в тензорной форме в декартовой системе координат
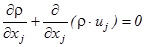
где нижний индекс j в соответствии с тремя пространственными координатами принимает значения 1, 2, 3. Повторение этого индекса дважды обозначает суммирование трех аналогичных членов, например
Одно из достоинств тензорной записи в декартовой системе координат заключается в том, что одномерный вид уравнения можно получить, если просто опустить индекс j.
Процедура записи дифференциального уравнения в обобщенном виде заключается в его преобразовании до тех пор, пока нестационарный, диффузионный и источниковый члены уравнения для данной зависимой переменной не примут стандартный вид. Тогда в качестве выражения для Г берут коэффициент перед 
в диффузионном члене, а все оставшиеся члены в правой части обозначают S (источниковый член).
До сих пор мы рассматривали размерные переменные, однако иногда удобнее иметь дело с безразмерными величинами. При этом также можно считать, что каждое из дифференциальных уравнений, записанное через безразмерные переменные, можно представить в обобщенном виде, где Ф — безразмерная зависимая переменная, а Г и S — безразмерные коэффициент диффузии и источниковый член. Во многих случаях безразмерный коэффициент Г= 1, a S принимает значения 0 либо 1.
Тот факт, что все интересующие нас дифференциальные уравнения, описывающие тепло- и массообмен, гидродинамику и турбулентность, можно рассматривать как частные случаи обобщенного уравнения для Ф, позволяет ограничиться численным решением обобщенного уравнения. Следовательно, при создании программы расчета достаточно записать общую последовательность операций для решения обобщенного уравнения, которую можно применять для нахождения различных Ф при использовании соответствующих выражений для Г и S и, конечно, соответствующих начальных и граничных условий. Таким образом, концепция обобщенного уравнения позволяет сформулировать обобщенный численный метод и подготовить многоцелевые программы расчета.
