Каждое из рассматриваемых здесь дифференциальных уравнений представляет собой закон сохранения какой-либо физической величины. Обычно зависимыми переменными в этих дифференциальных уравнениях являются удельные свойства, т.е. отнесенные к единице массы. Примерами являются массовая концентрация, скорость, удельная энтальпия.
Вопрос: какая величина не является удельным свойством, но которая часто используется?
Члены дифференциального уравнения такого типа выражают воздействие на единицу объема. Пусть 
поток некоторой переменной Ф.
Рассмотрим объем
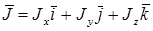
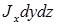- поток, втекающий через грань
- вытекающий поток
Разность между втекающим и вытекающим потоком:
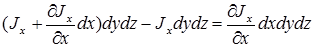
Аналогично для двух других осей можем получить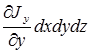 
, 
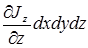. Замечая что 
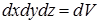- объем, получим чистое истечение на единицу объема
Такая интерпретация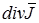 
особенно полезна ввиду того, что, как будет видно ниже, построение численного метода будет выполняться на основе принципа баланса для контрольного объема. К единице объема относиться также член 
, который описывает скорость изменения соответствующего свойства в единице объема.
