Степенным рядом называют ряд вида:
,
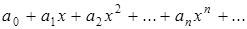где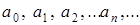 
– постоянные числа (коэффициенты ряда).
Интервал сходимости степенного ряда можно находить с помощью признака Даламбера, т.е. находим 
. Известно, что ряд сходится при 
, расходится при 
, а при 
необходимы дополнительные исследования.
Пример.
Определить интервал сходимости ряда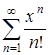 
.
Решение.
Выпишем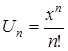 
, 
, тогда:
.
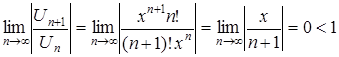Таким образом, ряд сходится при любых 
.
Пример.
Определить интервал сходимости ряда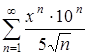 
.
Решение.
Выпишем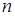 
-ный и 
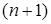-ый члены ряда:
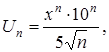
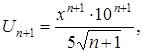
тогда:
.
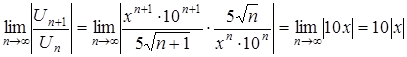Ряд будет сходящимся, если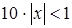 
. Отсюда 
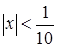, т.е. исходный ряд сходится на интервале 
.
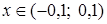Контрольная работа
В задачах 1.1 – 1.35 найти пределы
| 1.1. | 1.2. |
а)  ;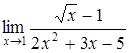
| а)  ;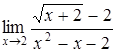
|
б)  ;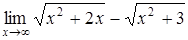
| б)  ;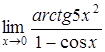
|
в)  ;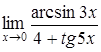
| в)  ;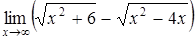
|
г)  .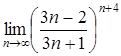
| г)  .
|
| 1.3. | 1.4. |
а)  ;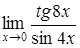
| а)  ;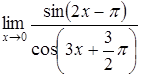
|
б)  ;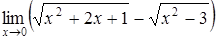
| б)  ;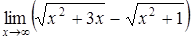
|
в)  ;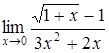
| в)  ;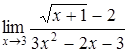
|
г)  .
| г)  .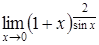
|
| 1.5. | 1.6. |
а)  ;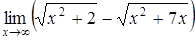
| а)  ;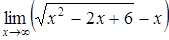
|
б)  ;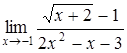
| б)  ;
|
в)  ;
| в)  ;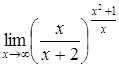
|
г)  .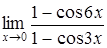
| г)  .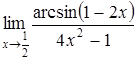
|
| 1.7. | 1.8. |
а)  ;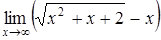
| а)  ;
|
б)  ;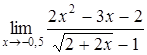
| б)  ;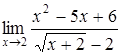
|
в)  ;
| в)  ;
|
г)  .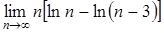
| г)  .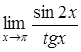
|
| 1.9. | 1.10. |
а)  ;
| а)  ;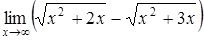
|
б)  ;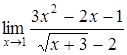
| б)  ;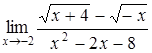
|
в)  ;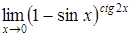
| в)  ;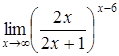
|
г)  .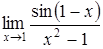
| г)  .
|
| 1.11. | 1.12. |
а)  ;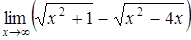
| а)  ;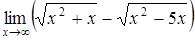
|
б)  ;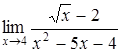
| б)  ;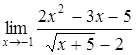
|
в)  ;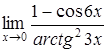
| в)  ;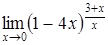
|
г)  .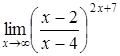
| г)  .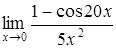
|
| 1.13. | 1.14. |
а)  ;
| а)  ;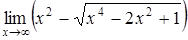
|
б)  ;
| б)  ;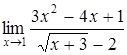
|
в)  ;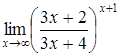
| в)  ;
|
г)  .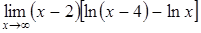
| г)  .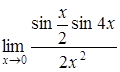
|
| 1.15. | 1.16. |
а)  ;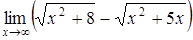
| а)  ;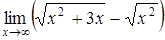
|
б)  ;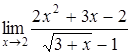
| б)  ;
|
в)  ;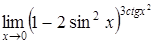
| в)  ;
|
г)  .
| г)  .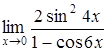
|
| 1.17. | 1.18. |
а)  ;
| а)  ;
|
б)  ;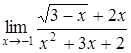
| б)  ;
|
в)  ;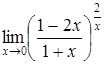
| в)  ;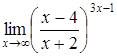
|
г)  .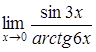
| г)  .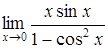
|
| 1.19. | 1.20. |
а)  ;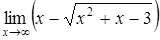
| а)  ;
|
б)  ;
| б)  ;
|
в)  ;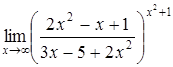
| в)  ;
|
г)  .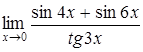
| г)  .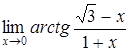
|
| 1.21. | 1.22. |
а)  ;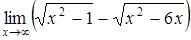
| а)  ;
|
б)  ;
| б)  ;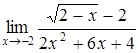
|
в)  ;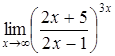
| в)  ;
|
г)  .
| г)  .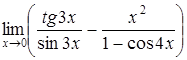
|
| 1.23. | 1.24. |
а)  ;
| а)  ;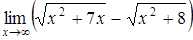
|
б)  ;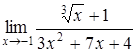
| б)  ;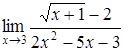
|
в)  ;
| в)  ;
|
г)  .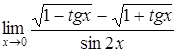
| г)  .
|
| 1.25. | 1.26. |
а)  ;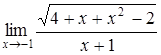
| а)  ;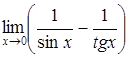
|
б)  ;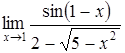
| б)  ;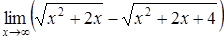
|
в)  ;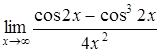
| в)  ;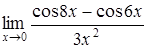
|
г)  .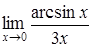
| г)  .
|
| 1.27. | 1.28. |
а)  ;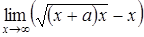
| а)  ;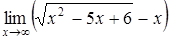
|
б)  ;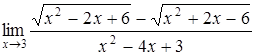
| б)  ;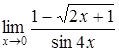
|
в)  ;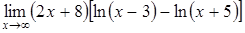
| в)  ;
|
г)  .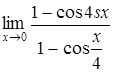
| г)  .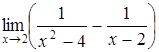
|
| 1.29. | 1.30. |
а)  ;
| а)  ;
|
б)  ;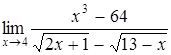
|
б)  ;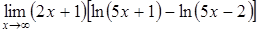
|
в)  ;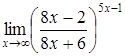
| в)  ;
|
г)  .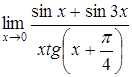
| г)  .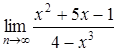
|
| 1.31. | 1.32. |
а)  ;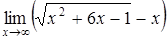
| а)  ;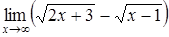
|
б)  ;
| б)  ;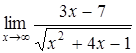
|
в)  ;
| в)  ;
|
г)  .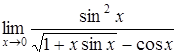
| г)  .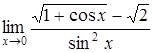
|
| 1.33. | 1.34. |
а)  ;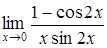
| а)  ;
|
б)  ;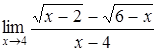
| б)  ;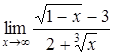
|
в)  ;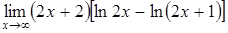
| в)  ;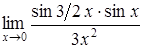
|
г)  .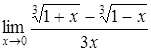
|
г)  .
|
| 1.35. |
а)  ;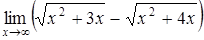
|
б)  ;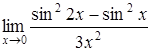
|
в)  ;
|
г)  .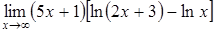
|
В задачах 2.1. –2.35 вычислить производную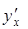 
.
| 2.1. | ||
а)  ;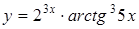
| б)  ;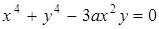
| в)  .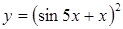
|
| 2.2. | ||
а)  ;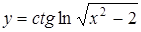
| б)  ;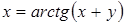
| в)  .
|
| 2.3. | ||
а)  ;
| б)  ;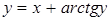
| в)  .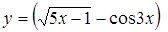
|
| 2.4. | ||
а)  ;
| б)  ;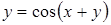
| в)  .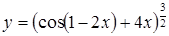
|
| 2.5. | ||
а)  ;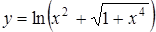
| б)  ;
| в)  .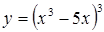
|
| 2.6. | ||
а)  ;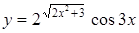
| б)  ;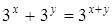
| в)  .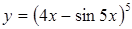
|
| 2.7. | ||
а)  ;
| б)  ;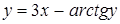
| в)  .
|
| 2.8. | ||
а)  ;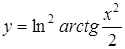
| б)  ;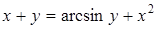
| в)  .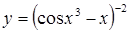
|
| 2.9. | ||
а)  ;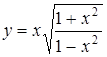
| б)  ;
| в)  .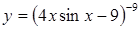
|
| 2.10. | ||
а)  ;
| б)  ;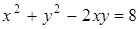
| в)  .
|
| 2.11. | ||
а)  ;
| б)  ;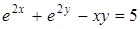
| в)  .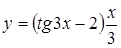
|
| 2.12. | ||
а)  ;
| б)  ;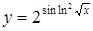
| в)  .
|
| 2.13. | ||
а)  ;
| б)  ;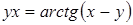
| в)  .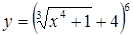
|
| 2.14. | ||
а)  ;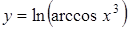
| б)  ;
| в)  .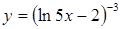
|
| 2.15. | ||
а)  ;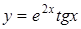
| б)  ;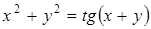
| в)  .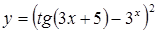
|
| 2.16. | ||
а)  ;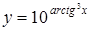
| б)  ;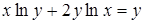
| в)  .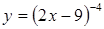
|
| 2.17. | ||
а)  ;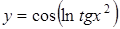
| б)  ;
| в)  .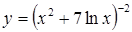
|
| 2.18. | ||
а)  ;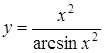
| б)  ;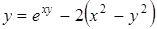
| в)  .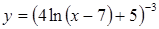
|
| 2.19. | ||
а)  ;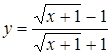
| б)  ;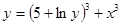
| в)  .
|
| 2.20. | |||
а)  ;
| б)  ;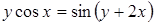
| в)  .
| |
| 2.21. | |||
а)  ;
| б)  ;
| в)  .
| |
| 2.22. | |||
а)  ;
| б)  ;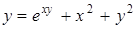
| в)  .
| |
| 2.23. | |||
а)  ;
| б)  ;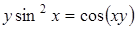
| в)  .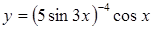
| |
| 2.24. | |||
а)  ;
| б)  ;
| в)  .
| |
| 2.25. | |||
а)  ;
| б)  ;
| в)  .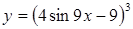
| |
| 2.26. | |||
а)  ;
| б)  ;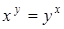
| в)  .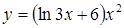
| |
| 2.27. | |||
а)  ;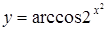
| б)  ;
| в)  .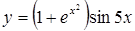
| |
| 2.28. | |||
а)  ;
| б)  ;
| в)  .
| |
| 2.29. | |||
а)  ;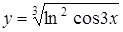
| б)  ;
| в)  .
| |
| 2.30. | |||
а)  ;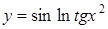
| б)  ;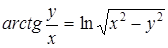
| в)  .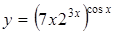
| |
| 2.31. | |||
а)  ;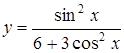
| б)  ;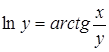
| в)  .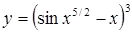
| |
| 2.32. | |||
а)  ;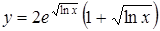
| б)  ;
| в)  .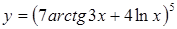
| |
| 2.33. | |||
а)  ;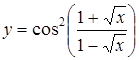
| б)  ;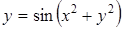
| в)  .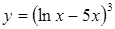
| |
| 2.34. | |||
а)  ;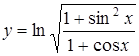
| б)  ;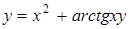
| в)  .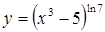
| |
| 2.35. | |||
а)  ;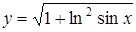
| б)  ;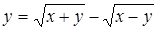
| в)  .
| |
В задачах 3.1.-3.35. исследовать средствами дифференциального исчисления функцию. Найти асимптоты и построить график.
3.1.  ;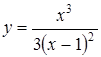
| 3.2.  ;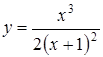
| 3.3.  ;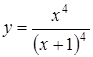
| |
3.4.  ;
| 3.5.  ;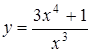
| 3.6.  ;
| |
3.7.  ;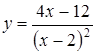
| 3.8.  ;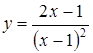
| 3.9.  ;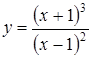
| |
3.10.  ;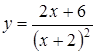
| 3.11.  ;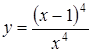
| 3.12.  ;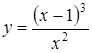
| |
3.13.  ;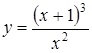
| 3.14.  ;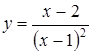
| 3.15.  ;
| |
3.16.  ;
| 3.17.  ;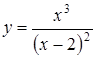
| 3.18.  ;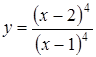
| |
3.19.  ;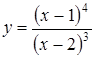
| 3.20.  ;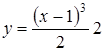
| 3.21.  ;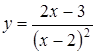
| |
3.22.  ;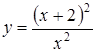
| 3.23.  ;
| 3.24. ;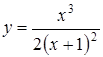
| |
3.25.  ;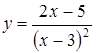
| 3.26.  ;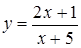
| 3.27.  ;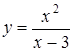
| |
3.28.  ;
| 3.29.  ;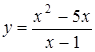
| 3.30.  ;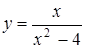
| |
3.31.  ;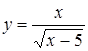
| 3.32.  ;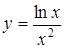
| 3.33.  ;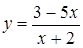
| |
3.34.  ;
| 3.35.  .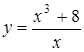
| ||
В задачах 4.1.- 4.35 вычислить интегралы.
| 4.1. | а)  ;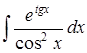
| б)  ;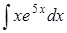
|
в)  ;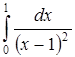
| г)  .
|
| 4.2. | а)  ;
| б)  ;
|
в)  ;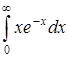
| г)  .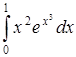
|
| 4.3. | а)  ;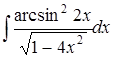
| б)  ;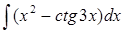
|
в)  ;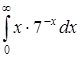
| г)  .
|
| 4.4. | а)  ;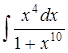
| б)  ;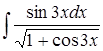
|
в)  ;
| г)  .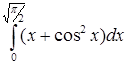
|
| 4.5. | а)  ;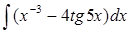
| б)  ;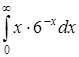
|
в)  ;
| г)  .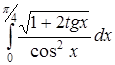
|
| 4.6. | а)  ;
| б)  ;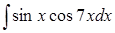
|
в)  ;
| г)  .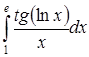
|
| 4.7. | а)  ;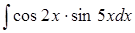
| б)  ;
|
в)  ;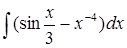
| г)  .
|
| 4.8. | а)  ;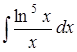
| б)  ;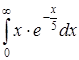
|
в)  ;
| г)  .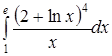
|
| 4.9. | а)  ;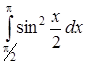
| б)  ;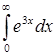
|
в)  ;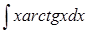
| г)  .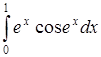
|
| 4.10. | а)  ;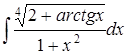
| б)  ;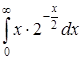
|
в)  ;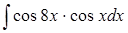
| г)  .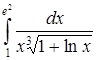
|
| 4.11. | а)  ;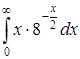
| б)  ;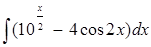
|
в)  ;
| г)  .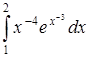
|
| 4.12. | а)  ;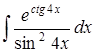
| б)  ;
|
в)  ;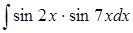
| г)  .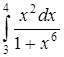
|
| 4.13. | а)  ;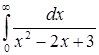
| б)  ;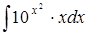
|
в)  ;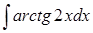
| г)  .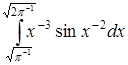
|
| 4.14. | а)  ;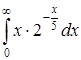
| б)  ;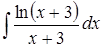
|
в)  ;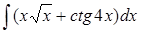
| г)  .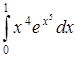
|
| 4.15. | а)  ;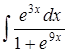
| б)  ;
|
в)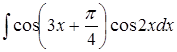 
| г)  .
|
| 4.16. | а)  ;
| б)  ;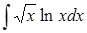
|
в)  ;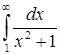
| г)  .
|
| 4.17. | а)  ;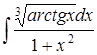
| б)  ;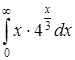
|
в)  ;
| г)  .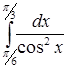
|
| 4.18. | а)  ;
| б) 
|
в)  ;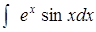
| г)  .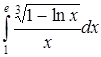
|
| 4.19. | а)  ;
| б)  ;
|
в)  ;
| г)  .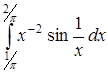
| |
| 4.20. | а)  ;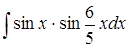
| б)  ;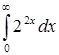
|
в)  ;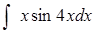
| г)  .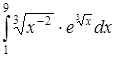
|
| 4.21. | а)  ;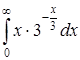
| б)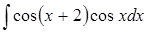 
|
в)  ;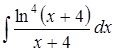
| г)  .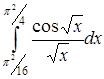
|
| 4.22. | а)  ;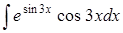
| б)  ;
|
в)  ;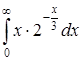
| г)  .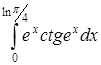
|
| 4.23. | а)  ;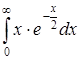
| б)  ;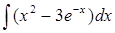
|
в)  ;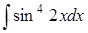
| г)  .
|
| 4.24. | а)  ;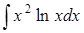
| б)  ;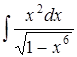
|
в)  ;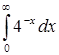
| г)  .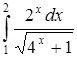
|
| 4.25. | а)  ;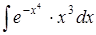
| б)  ;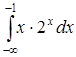
|
в)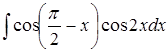 
| г) .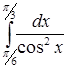
|
| 4.26. | а)  ;
| б)  ;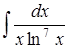
|
в)  ;
| г)  .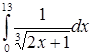
|
| 4.27. | а)  ;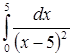
| б)  ;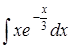
|
в)  ;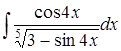
| г)  .
|
| 4.28. | а)  ;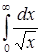
| б)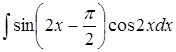 
|
в)  ;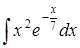
| г)  .
|
| 4.29. | а)  ;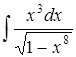
| б)  ;
|
в)  ;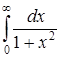
| г)  .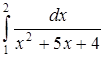
|
| 4.30. | а)  ;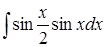
| б)  ;
|
в)  ;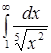
| г)  .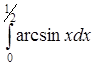
|
| 4.31. | а)  ;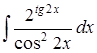
| б)  ;
|
в)  ;
| г)  .
|
| 4.32. | а)  ;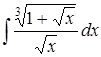
| б)  ;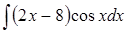
|
в)  ;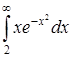
| г)  .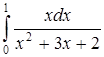
|
| 4.33. | а)  ;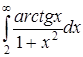
| б) 
|
в)  ;
| г)  .
|
| 4.34. | а)  ;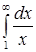
| б)  ;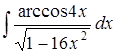
|
в)  ;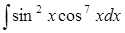
| г)  .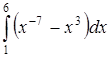
|
| 4.35. | а)  ;
| б)  ;
|
в)  ;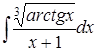
| г)  .
|
В задачах 5.1- 5.35 решить дифференциальные уравнения:
| 5.1. | ||
а)  ;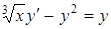
| б)  ;
| в)  .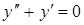
|
| 5.2. | ||
а)  ;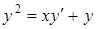
| б)  ;
| в)  .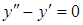
|
| 5.3. | ||
а)  ;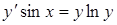
| б)  ;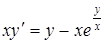
| в)  .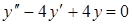
|
| 5.4. | ||
а)  ;
| б)  ;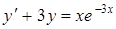
| в)  .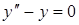
|
| 5.5. | ||
а)  ;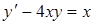
| б)  ;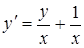
| в)  .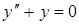
|
| 5.6. | ||
а)  ;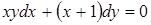
| б)  ;
| в)  .
|
| 5.7. | ||
а)  ;
| б)  ;
| в)  .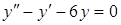
|
| 5.8. | ||
а)  ;
| б)  ;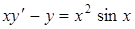
| в)  .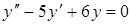
|
| 5.9. | ||
а)  ;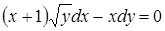
| б) ;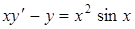
| в)  .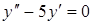
|
| 5.10. | ||
а)  ;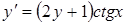
| б)  ;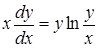
| в)  .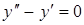
|
| 5.11. | ||
а)  ;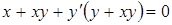
| б)  ;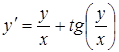
| в) .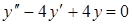
|
| 5.12. | ||
а)  ;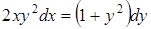
| б)  ;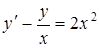
| в)  .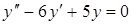
|
| 5.13. | ||
а)  ;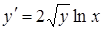
| б)  ;
| в)  .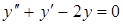
|
| 5.14. | ||
а)  ;
| б)  ;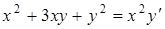
| в)  .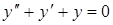
|
| 5.15. | ||
а)  ;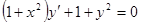
| б)  ;
| в) .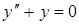
|
| 5.16. | ||
а)  ;
| б)  ;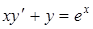
| в)  .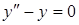
|
| 5.17. | ||
| а) | ||
|
|
|
|
|
|
Дата добавления: 2016-11-12; Мы поможем в написании ваших работ!; просмотров: 453 | Нарушение авторских прав
Лучшие изречения:
| 2189 - 