Так как интегрирование многочлена не представляет трудностей, то достаточно научиться интегрировать правильные рациональные дроби. Сформулированная ниже теорема позволяет свести интегрирование любой правильной рациональной дроби к интегрированию элементарных дробей.
Теорема. Если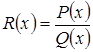 
- правильная рациональная дробь, знаменатель 
которой представлен в виде произведения линейных и квадратичных множителей (с действительными коэффициентами):
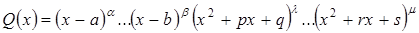(3.3)
то эта дробь может быть разложена на элементарные дроби по следующей схеме:
(3.4)
где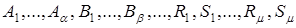 
- некоторые действительные числа.
Практически разложение конкретной правильной рациональной дроби 
на сумму элементарных дробей обычно производят методом неопределенных коэффициентов. Для этого:
§ разлагают знаменатель на произведение линейных и квадратичных множителей;
§ записывают разложение дроби по схеме (3.4) с неопределенными коэффициентами;
§ приводят элементарные дроби к общему знаменателю ;
§ приравнивают многочлен, получившийся в числителе, к многочлену 
.
Для того чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы коэффициенты при одинаковых степенях 
у них были равны. Учитывая это замечание, приравниваем коэффициенты при одинаковых степенях в левой и правой частях равенства, получая тем самым систему алгебраических уравнений для нахождения неопределенных коэффициентов.
Существование такой системы вытекает из сформулированной выше теоремы.
Примеры.
1. 
.
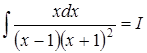Решение.
Имеем:
.
Отсюда:
. (*)
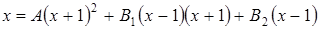а) Первый способ определения коэффициентов.
Перепишем тождество (*) в виде:
.
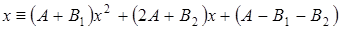Приравнивая коэффициенты при одинаковых степенях , получим:
.
Отсюда:
; 
; 
.
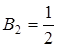б) Второй способ определения коэффициентов.
Полагая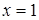 
в тождестве (*), будем иметь: 
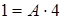, т.е. .
Полагая 
, получим: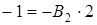 
, т.е. .
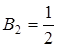Далее, полагая 
, будем иметь: 
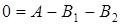, т.е. .
Следовательно:
.
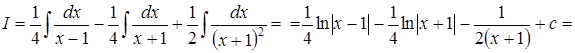
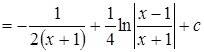2. Найти: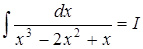 
.
Решение.
Имеем:
;
;
;
;
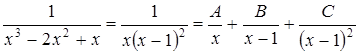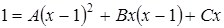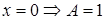, т.е. 
.
Таким образом: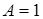 
, и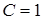 
.
Следовательно:
.
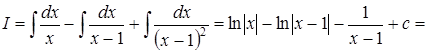
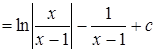Интегрирование тригонометрических выражений
Рассмотрим интеграл следующего вида:
.
1. Если 
(нечетное), тогда полагают:
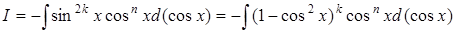
и делают замену 
;
2. Если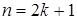 
(нечетное), тогда полагают:
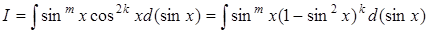
и делают замену 
;
3. Если 
и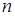 
- четные, то преобразуют с помощью формул:
, 
, 
;
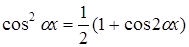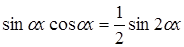4. Если и 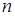- целые отрицательные числа одинаковой четности (
, 
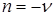), тогда полагают:
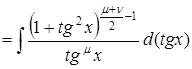
и делают замену 
.
Интегралы вида:
, 
, 
,
вычисляются при помощи формул:
;
;
.
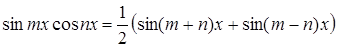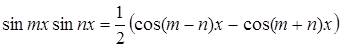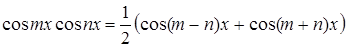При интегрировании тригонометрических выражений также применяют универсальную подстановку 
.
ІV. Дифференциальные уравнения
Основные понятия
Обыкновенным дифференциальным уравнением называется уравнение, связывающее искомую функцию одной переменной и производные различных порядков данной функции.
В общем случае дифференциальное уравнение можно записывать в виде:
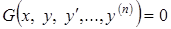(4.1)
при этом порядок 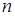старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения.
Решением дифференциального уравнения (4.1) называется такая функция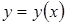 
, которая при подстановке ее в это уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Общим решением дифференциального уравнения (4.1) 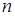-го порядка называется такое его решение:
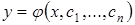(4.2)
которое является функцией переменной и 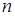произвольных независимых постоянных 
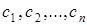. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
Частным решение дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных .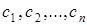
К дифференциальным уравнениям приводят многие задачи экономики, физики, биологии, экологии и т.п.
v Уравнения, интегрируемые непосредственно.
Дифференциальное уравнение 1-го порядка называется уравнением, интегрируемым непосредственно, если оно может быть представлено в виде:
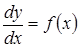(4.3)
или в виде:
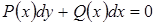(4.4)
где 
, , - некоторые функции переменной .
В этом случае уравнение (4.3) можно проинтегрировать непосредственно, т. е.
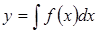(4.5)
Уравнение (4.4) можно привести к виду (4.3):
,
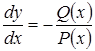тогда
. (4.6)
Пример
Решить уравнение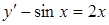 
.
Решение.
.
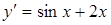Проинтегрируем непосредственно:
.
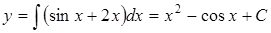Итак,
.
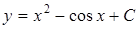Пример
Решить уравнение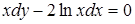 
.
Решение.
Преобразуем уравнение:
;
.
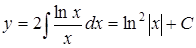Итак,
.
