Пусть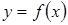 
задана на интервале 
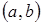. Возьмем некоторую точку 
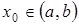и придадим ей приращение 
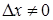так, чтобы 
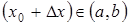. Если существует конечный предел 
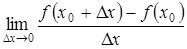, то его называют производной функции 
в точке 
. Если такой предел существует в каждой точке 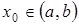, то он называется производной от функции на . Операция нахождения производной от функции называется дифференцированием.
Для обозначения производной в точке 
используются символы:
.
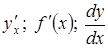Правила дифференцирования.
1. Если функции 
и 
дифференцируемы в точке , то в точке дифференцируемы 
функции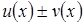 
, 
, 
, 
, 
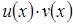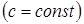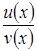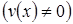и справедливы формулы:
§ 
;
§ 
;
§ 
;
§ 
.
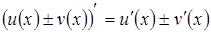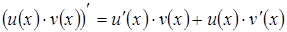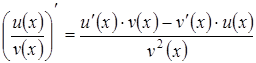2. Производная сложной функции: если дифференцируема в точке 
, то сложная функция 
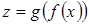дифференцируема в точке и справедлива формула:
,
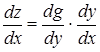т.е. производная сложной функции 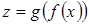равна произведению производной внешней функции 
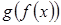на производную внутренней функции .
Замечание. Правило нахождения производной сложной функции распространяется на композицию любого конечного числа функций. Например, для вычисления производной функции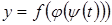 
, если 
, 
, 
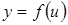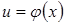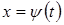дифференцируемы, справедлива формула:
.
Приведем таблицу производных основных элементарных функций:
| Функция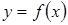
| Производная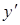 
|
| 
|
| 
|
| 
|
| 
|
 , 
| 
|
| 
|
 ,
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
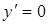
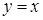
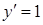
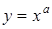
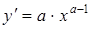
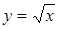
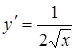
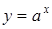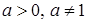
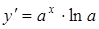
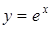
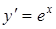
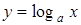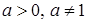
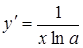
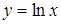
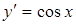
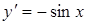
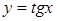
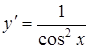
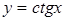
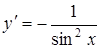
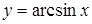
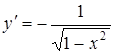
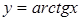
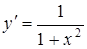
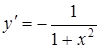
Рассмотрим решение примеров.
Пример № 1.
.
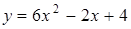Решение.
Пользуясь таблицей производных и свойствами производных, имеем:
.
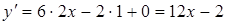Пример № 2.
Найти производную 
.
Решение.
.
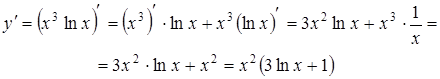Пример № 3.
Найти производную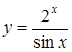 
.
Решение.
.
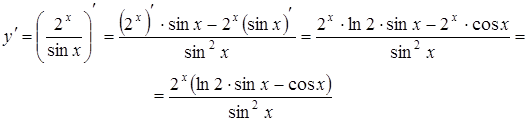Пример № 4.
Найти производную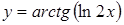 
.
Решение. Так как функция 
является сложной вида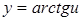 
, где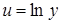 
, 
, то имеем:
.
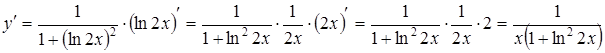Пример № 5.
Найти производную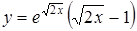 
.
Решение.
.
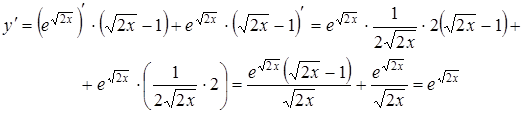Производные высших порядков
Пусть функция задана на 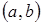и в каждой точке 
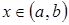существует 
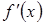. Тогда мы имеем новую функцию 
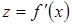, заданную на 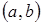, называемую производной функции . Значит, имеет смысл говорить о производной функции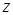 
, то есть о 
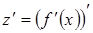или о второй производной от функции , которая обозначается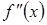 
, 
, 
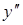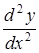. И, обобщая данную ситуацию, можно сказать, что производной 
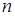-го порядка от функции называется производная от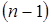 
-ой производной функции :
, 
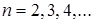
Дифференцирование некоторых функций
Дифференцирование неявных функций.
Пусть уравнение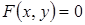 
определяет как неявную функцию от . В дальнейшем будем считать эту функцию дифференцируемой.
Продифференцировав по обе части уравнения 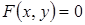, получим уравнение первой степени относительно 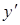. Из этого уравнения легко находится 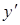, т.е. производная неявной функции.
Пример № 1.
Найти производную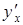 
из уравнения 
.
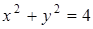Решение.
Так как является функцией от , то будем рассматривать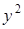 
как сложную функцию от . Следовательно, 
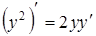. Продифференцировав по обе части данного уравнения, получим: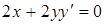 
, т.е. 
.
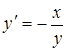Пример № 2.
Найти производную 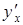из уравнения 
.
Решение.
Дифференцируя по обе части уравнения, получим:
,
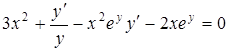т.е.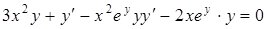 
.
Перенесём в одну сторону равенства все слагаемые, содержащие 
, тогда:
,
,
.
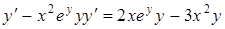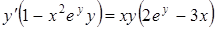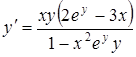Дифференцирование степенно-показательной функции: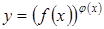 
.
Чтобы вычислить производную данной функции применятся специальный прием: предварительно прологарифмируем данное равенство по основанию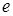 
, а затем продифференцируем по аргументу , учитывая, что функция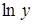 
сложная.
Пример № 3.
;
;
;
;
;
;
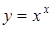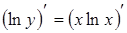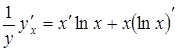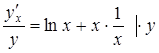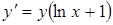наконец: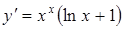 
.
Замечание. Способ дифференцирования функции предварительным логарифмированием также эффективен при нахождении производной функции, являющейся произведением или частным нескольких функций.
Пример № 4.
Найти производную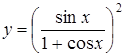 
.
Решение.
Прологарифмируем обе части уравнения по основанию :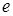
; 
; 
;
; 
;
;
.
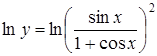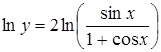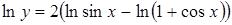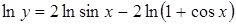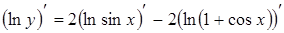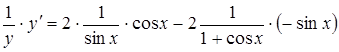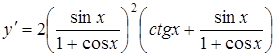