Математическое ожидание случайной величины, имеющей плотность вероятности.

Пусть плотность распределения случайной величины есть . Разобьем числовую ось на малые отрезки точками х_к, где , и положим

(рис. 2).

 

 

 

Определим новую дискретную случайную величину 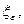принимающую значения х_к по одному в каждом отрезке причем вероятность значения х_к равна вероятности попадания величины ξ в отрезок [ х_к,х_{к+ 1}]

= .

Условие , обязательное для дискретного распределения, выполняется, поскольку

.

Случайную величину будем называть - приближением к случайной величине ξ.

Замечание. Если величина ξ связана с некоторым опытом, то взаимоотношения между ξ и можно истолковать следующим образом. Пусть произведен опыт, и в результате его величина ξ приняла значение, принадлежащее некоторому промежутку [ х_к,х_{к +1}] (x [ х_к,х _к+1]). Тогда величина по определению принимает в том же опыте значения . При таком определении события ( = x_к) и (ξ [ х_к,х_{к +1}]) будут равны, и следовательно будут совпадать и вероятности этих событий. Это как раз и соответствует данному выше определению величины . Итак величина получается путем округления значений, принимаемых величиной ξ, до ближайшей слева точки х_к отрезка [ х_к,х_{к +1}], куда попадает это значение.

Отсюда, между прочим, видно, что переход от случайной величины ξ к дискретной случайной величине имеет вполне реальный смысл. Например, такой переход совершается всякий раз, когда значения величины ξ считываются с измерительного прибора, причём показания прибора округляются до ближайшего слева деления шкалы.

Наши рассуждения показывают, что по мере приближения к нулю различие между и ξ становятся все менее существенными. Поэтому естественно принять такое определение.

Определение. Математическим ожиданием случайной величины ξ называется число

.

Если указанный предел не существует, то математическое ожидание величины ξ также считается несуществующим.

Итак мы получаем.

Mξ = . (1*)

Покажем, что предел в (1*) равен

. (2*)

Сравним по модулю к -ые члены рядов (1*) и (2*)

Следовательно

Итак, мы получили следующую формулу для математического ожидания величины

Мξ = (7)

Заметим, что мы использовали формулу математического ожидания для ДСВ

, (2*)

а она будет верна (см. определение 1) если ряд (2*) будет абсолютно сходится. Далее, для сходимости ряда достаточно требовать сходимости интеграла

.

Таким образом мы получили.

Теорема 1. Пусть ξ – непрерывная случайная величина распределённая с плотностью p (x). Если сходится интеграл , то существует Mξ и справедлива формула

M ξ= . (8)

Аналогично теореме 1, доказывается теорема 2.

Теорема 2. Пусть ξ - непрерывная случайная величина, распределённая с плотностью p (x).Если сходится интеграл , то существует математическое ожидание Mφ(ξ) случайной величины φ(ξ) и имеет место формула.

M = . (9)

 

Пример 1. Найти математическое ожидание случайной величины ξ, равномерно распределённой на отрезке [ a, b ].

 

Решение. Имеем.

 

Мы получили, таким образом, что числу Mξ соответствует середина отрезка [ a,b ]. Ввиду равномерности распределения ξ на отрезке [ a, b ] такой ответ ожидаем.

Можно показать, что математическое ожидание случайной величины , распределенной по нормальному закону с плотностью

= , (10)

равно параметру а, входящего в выражение (10) для нормального закона.

Пример 2. Распределение Коши. Плотность распределения Коши имеет вид

= .

Значит

M

Этот интеграл не является абсолютно сходящимся, и, значит, среднее значение для распределения Коши не существует.

Чтобы сделать аппарат числовых характеристик более эффективным, необходимо изучить их свойства. Приведём свойства математического ожидания.

 

Основные свойства математического ожидания.

1. Если случайная величина может принимать только одно значение С, то

 

M ξ =МС=С. (11)

 

Действительно, постоянную величину ξ=С можно рассматривать, как дискретную величину, принимающую только одно постоянное значение х₁ =С с вероятностью 1. Но тогда M ξ =С ·1= С.

2. Постоянный множитель C можно выносить за знак математического ожидания:

 

M(C )=СM

 

Для ДСВ равенство (12) очевидно. Справедливость формулы для произвольной случайной величины (имеющей математическое ожидание) теперь легко вытекает из общего определения математического ожидания.

3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

 

M(ξ₁+ξ₂) = 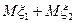. (13)

 

Докажем свойство (13) для ДСВ . Пусть - возможные значения величины ξ ₁ и …- возможные значения ξ ₂. Возможные значения величины ξ = ξ ₁+ ξ ₂ будут содержаться среди чисел z вида x_i+y_j причем

 

,

где есть вероятность события (ξ ₁= x_i, ξ ₂= y_j) (см. §5). Значит

M .

Здесь суммирование сначала производится по тем парам (i,j), для которых x_i+y_j=z_k; поэтому можно заменить во внутренней сумме z_k на x_i+y_j, т.е.

M .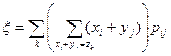

Затем суммирование производится по всем k, так что в итоге суммирование распределяется уже на все пары индексов (i,j), какова бы ни была сумма x_i+y_j, т.е.

 

В правой части (15) две суммы: в первой из них будем суммировать сначала по j, а затем по i, во второй – наоборот:

 

В силу формул (5) §5 гл.II

и значит

M .

Если ξ ₁ и ξ ₂ непрерывные случайные величины, имеющие плотности, то это свойство также доказывается, если использовать формулы композиции (5) из §6 гл.II.

Формула (13) переносится на любое конечное число слагаемых

 

M(ξ ₁ +…+ξ_n) =Mξ ₁ +…+M ξ_n.

 

4. Если случайные величины ξ ₁ и ξ ₂ независимы. То математическое ожидание их произведения равно произведению их математических ожиданий, т.е.

 

M(ξ₁ξ₂)=(Mξ₁)(Mξ₂). (16)

При доказательстве ограничимся случаем, когда система (ξ _1, ξ ₂ ) дискретного типа.

Если ξ ₁ и ξ ₂ – дискретны, то тогда для ξ = ξ ₁· ξ ₂ применив такие же рассуждения, как и при выводе формулы (15), получим равенство

M (ξ ₁· ξ ₂)= .

Ввиду независимости величин ξ ₁ и ξ ₂ имеем:

Обозначив,

,

получим

В правой части полученного равенства члены суммируются, в конечном счете, по всем возможным парам (i,j), суммируя сначала по j, а затем по i имеем:

что и требовалось доказать.

Найдем математическое ожидание биномиального распределения (см. пример 1.), используя свойство 3.

Рассмотрим схему Бернулли: Производится n независимых опытов. В каждом из них с одной и той же вероятностью p может появиться некоторое событие А. Требуется найти математическое ожидание случайной величины ξ - числа наступлений события А в n опытах.

Решение. Обозначим через ξ_i число наступлений события А в i - м опыте (i =1,2,..., n). Очевидно,

ξ=ξ₁+ξ₂+…+ ξ_n.

Закон распределения каждой из величин ξ ₁, ξ _2,…, ξ_n один и тот же.

 

Значение ξi
Вероятности	q	p

 

где q = . Следовательно Mξ_i= 0 q+ 1 ·p=p. По формуле сложения математических ожиданий имеем:

 

Mξ=Mξ₁+ Mξ₂+…+ Mξ_n = np. (17)

 

Пример 3. Случайное отклонение размера детали от стандарта подчиняется нормальному закону с параметрами a =0, σ=5мк. Годными считаются детали, для которых отклонение не превышает 10мк. Определить среднее число годных деталей из ста выбираемых наудачу.

Решение. Обозначим через А событие, состоящее в том, что деталь оказалась годной. Тогда (см. (12) §3 гл.II)

,

где ξ обозначает отклонение размера детали от стандарта. По условию выбирается 100 деталей. Если рассматривать выбор каждой детали как отдельный опыт, то можно сказать, что производится 100 опытов. Нас интересует среднее число (математическое ожидание) наступлений события А в этих опытах. Применив формулу (17), найдём, что это число равно