В § 2 мы говорили об устойчивости средних характеристик большого числа опытов, об устойчивости сумм вида
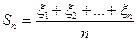 .
.
Однако величина Sn сама является случайной величиной, а значит имеет некоторый закон распределения.
Оказывается, что при весьма общих условиях закон распределения Sn близок к нормальному закону. Этим и определяется особая роль нормального распределения, поскольку с суммами большого числа случайных слагаемых приходится иметь дело весьма часто как в самой теории вероятностей, так и в её многочисленных приложениях.
В общих чертах содержание центральной предельной теоремы (кратко ЦПТ) может быть высказано следующим образом:
Распределение суммы большого числа независимых случайных величин, при весьма общих условиях, близко к нормальному распределению.
Перейдём к формулировке ЦПТ.
Пусть дана последовательность независимых величин 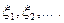 Составим «частичные» суммы» этих величин
Составим «частичные» суммы» этих величин
 (n =1,2…).
(n =1,2…).
От каждой из случайных величин  перейдем к, «нормированной» случайной величине
перейдем к, «нормированной» случайной величине
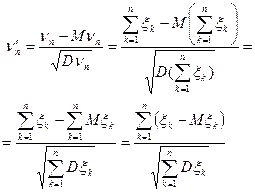
математическое ожидание которой равно 0, а дисперсия 1.
Действительно
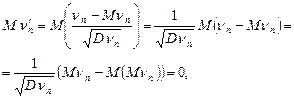
 .
.
Введём условие Ляпунова, налагаемое на последовательность 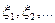 .
.
Условие Ляпунова. Если существует такое число δ>0, что
 ,
,
где 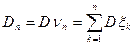 , то говорят, что последовательность случайных величин удовлетворяет условию Ляпунова.
, то говорят, что последовательность случайных величин удовлетворяет условию Ляпунова.
Условие Ляпунова является одним из возможных математических выражений того факта, что отдельные отклонения 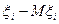 должны быть при больших n малы по сравнению с суммарным отклонением
должны быть при больших n малы по сравнению с суммарным отклонением 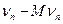 .
.
Проверим, в частности, что условие Ляпунова выполняется для одинаково распределенных слагаемых 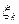 .
.
В этом случае все М 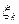 совпадают и равны некоторому числу m, все
совпадают и равны некоторому числу m, все  совпадают и равны некоторому d,
совпадают и равны некоторому d, 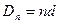 , все
, все 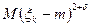 совпадают и равны некоторому b. Тогда
совпадают и равны некоторому b. Тогда
 .
.
И, значит, условие Ляпунова выполнено.
Теперь мы можем сформулировать ЦПТ в форме
А.М. Ляпунова.
Теорема. Если последовательность независимых случайных величин 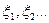 удовлетворяет условию Ляпунова, то для любых (конечных или бесконечных) a и b справедливо предельное соотношение
удовлетворяет условию Ляпунова, то для любых (конечных или бесконечных) a и b справедливо предельное соотношение
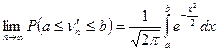 . (1)
. (1)
Иначе говоря, в этом случае закон распределения нормированной суммы  сходится к нормальному закону с параметрами: m =0,
сходится к нормальному закону с параметрами: m =0,  =1.
=1.
Замечание о роли нормального закона.
Допустим, что производится измерение какой либо физической величины. На результат измерения влияет огромное количество случайных факторов, таких, как колебание атмосферных условий, сотрясение измерительного прибора, личные особенности наблюдателя и т.д. Каждый из этих факторов, взятых в отдельности, порождает ничтожную ошибку ξi в измерении данной величины. Все такие незначительные ошибки суммируются, так, что суммарная ошибка ν представляется в виде суммы большого числа случайных величин ξк с малыми значениями; часто можно считать ξк независимыми. И хотя закон распределения каждой из этих величин нам неизвестен, тем не менее (в виду ЦПТ) можно уверенно заключить, что вся сумма ν будет иметь закон распределения близкий к нормальному.
Исходя из сказанного выше, при математической обработке результатов измерения исходят из следующего постулата: случайная ошибка измерения подчиняется нормальному закону распределения. Из двух параметров этого закона один, а именно математическое ожидание, равен нулю. Второй параметр – среднее квадратичное отклонение – характеризует, в известном смысле, точность измерений.
Другой важный пример, характеризующий роль нормального распределения в приложениях теории вероятностей, дает массовое производство, существующее во многих отраслях современной промышленности. В процессе массового производства изготавливаются большие партии однотипных изделий. Все наиболее существенные характеристики выпускаемых изделий должны, естественно, соответствовать определенному стандарту однако в действительности наблюдаются отклонения от стандарта, которые порождаются причинами случайного характера (следует, учесть, что выпуск изделия связан, как правило, с большим числом операций, некоторые из них не могут быть выполнены абсолютно точно). Каждая из этих причин сама по себе порождает ничтожную ошибку ξi (это и есть, в каком то смысле, условие Ляпунова, что «достаточно вероятные» значения слагаемых ξк должны быть при больших n малы по сравнению со всей суммой ν n), но, складываясь, такие ошибки могут давать вполне ощутимые отклонения от стандарта. И здесь, так же как в случае ошибок измерения, имеются все основания считать, что суммарное отклонение от стандарта подчиняется нормальному распределению.
Подобных примеров можно привести много в разных областях науки и техники. Они объясняют, почему нормальный закон так часто возникает в задачах прикладного характера.
Приведём пример, иллюстрирующий ЦПТ.
Пример 1. Доска Гальтона.

Прибор Ф. Гальтона (1822-1911) состоит из слегка наклоненной прямоугольной доски в которую вбито в шахматном порядке большое число гвоздиков (рис.1) Сверху доски, в середине, помещается воронка, из которой выпускаются шарики: диаметр всех шариков одинаков и несколько меньше расстояния между гвоздиками. После столкновения с гвоздиками каждого ряда, шарик скатывается в одно из вертикальных отделений внизу доски, фиксирующих место выхода шарика из последнего ряда гвоздиков. Направим ось ОХ вдоль нижнего ребра доски, поместив начало в центре указанного ребра; за единицу масштаба примем расстояние между соседними гвоздиками.
При каждом столкновении шарик может пройти либо в левый, либо в правый просвет того же ряда гвоздиков.
Рассмотрим траекторию одного из шариков. Обозначим через ξ 1 смещение вдоль оси ОХ, полученное шариком между первым и вторым столкновениями с гвоздиками (при проходе через первый ряд гвоздиков), через ξ 2 – смещение полученное между вторым и третьим столкновениями, ξк – при проходе через к -ый ряд гвоздиков. Через ξ обозначим суммарное смещение, полученное после прохождения всех рядов гвоздиков, очевидно, имеем: ξ=ξ 1 +ξ 2 +…+ξn, где n число рядов.
Каждая из величин ξ 1, ξ 2, …, ξn представляет собой случайную величину, принимающую только два значения, +1 (проход шарика в правый просвет) и -1 (проход шарика в левый просвет), с вероятностями  ; её математическое ожидание равно 0, а дисперсия 1. Если n достаточно велико, то на основании ЦПТ (применённой к сумме большого числа одинаково распределенных независимых случайных величин), можно считать, что ξ имеет распределение, близкое к нормальному, с центром в точке 0 и средним квадратичным отклонением
; её математическое ожидание равно 0, а дисперсия 1. Если n достаточно велико, то на основании ЦПТ (применённой к сумме большого числа одинаково распределенных независимых случайных величин), можно считать, что ξ имеет распределение, близкое к нормальному, с центром в точке 0 и средним квадратичным отклонением  .Количество шариков в каждом отделении, согласно частотному смыслу вероятности, должно быть пропорционально вероятности попадания в отделения и тем самым соответствующей ординате плотности нормального распределения. Поэтому кривая «огибающая» лежащие в отделениях шарики отличается от нормальной кривой
.Количество шариков в каждом отделении, согласно частотному смыслу вероятности, должно быть пропорционально вероятности попадания в отделения и тем самым соответствующей ординате плотности нормального распределения. Поэтому кривая «огибающая» лежащие в отделениях шарики отличается от нормальной кривой 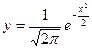 лишь постоянным множителем. Опыты показывают, что даже при не очень больших n расположение шариков отчётливо воспроизводит нормальную кривую.
лишь постоянным множителем. Опыты показывают, что даже при не очень больших n расположение шариков отчётливо воспроизводит нормальную кривую.
Применим теперь теорему Ляпунова к схеме Бернулли.
Пусть производится n независимых опытов, в каждом из которых с одной и той же вероятностью р (0< р <1) наступает
событие А. Рассмотрим случайную величину νn число наступления события А в n опытах. Очевидно,
νn= ξ 1 +ξ 2 +…+ξn,
где ξi обозначает число наступлений события А в i -м опыте (i =1,2,..., n). Случайные величины ξi имеют один и тот же закон распределения, так что условия теоремы Ляпунова выполнены. Но тогда должна быть справедлива формула (1), которая в данном случае принимает вид:
 (2)
(2)
(напомним, что 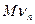 = np,
= np, 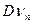 = npq см. §7,8 гл II).
= npq см. §7,8 гл II).
Это равенство носит название интегральной предельной теоремы Лапласа.
Покажем, что из него следует интегральная приближенная формула Лапласа (формула(3) §12 гл.II).
Событие
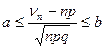
равнозначно
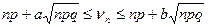
Положим
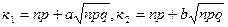 ,
,
так, что
 .
.
Тогда левая часть формулы (2) запишется:
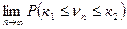 . (3)
. (3)
Правую же часть, учитывая соотношение: 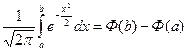 , (где Ф (x)-функция Лапласа), можно представить как
, (где Ф (x)-функция Лапласа), можно представить как
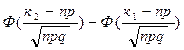 .
.
Приравнивая выражение, стоящее под знаком предела в (2), к выражению (3), получаем приближенное равенство
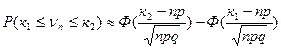 ,
,
которое есть не что иное, как интегральная приближённая формула Лапласа.






