При рассмотрении системы двух случайных величин (ξ,η) надо иметь в виду, что свойства системы не всегда исчерпываются свойствами самих величин ξ,η. Дело в том, что между величинами ξ,η, может существовать зависимость и без учёта этой зависимости нельзя построить закон распределения системы (ξ,η). В этом параграфе мы рассмотрим случай независимости случайных величин.
Определение. Случайные величины ξ1,ξ2,…ξn называются независимыми, если для любых борелевских множеств Bi выполняется равенство: 
(1)
Другими словами события:
независимы (см.§8 гл.1 определение 4). Если взять Bi = 
),то из (1), в случае независимости ξ1,…ξn, будет следовать равенство для многомерной функции распределения:
= 
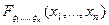(2)
Если распределение имеет плотность 
, то равенство (2) эквивалентно равенству (см (10) §5 гл.II)
= 
. (3)
Если случайные величины ξ 1,… ξn дискретны, то за определение независимости в этом случае можно принять равенство (см (1):
, (4)
где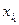 
,…, 
– возможные значения случайных величин ξ 1,…, ξn, соответственно.
Можно показать, что если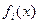 
есть непрерывные (или кусочно непрерывные) функции, то случайные величины 
также будут независимы.
Формула композиции. Пусть дана система двух случайных величин (ξ,η) с плотностью 
= p (x,y). Найдем закон распределения суммы ξ+η.
Функция распределения суммы ξ+η равна следующему интегралу:
, где G= ((x,y):x+y<z) есть полуплоскость с граничной прямой x+y=z (см рис.1 область G заштрихована).
Вычислим этот интеграл как повторный
Сделав замену переменных 
, получим
.
Итак, мы получили
.
Поскольку 
, то значит плотность распределения ξ+η выражается через плотность P(x,y) двумерного распределения (ξ,η) формулой
Рассмотрим случай, когда величины ξ и η независимы. Тогда в этом случае Pξ,η(x,y)=Pξ(x)Pη(y) и формула (5) принимает вид
В этом случае из формулы (6) следует, что
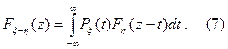
Формулы (6), (7) носят название формул композиции и свёртки. С помощью их мы выражаем плотность Pξ+η(z) и функцию распределения Fξ+η(z) суммы независимых случайных величин через плотности и функции распределения слагаемых.
Пример 1. Пусть ξ и η независимы, Fξ(х) функция распределения ξ, а η имеет плотность (равномерно распределена на [ a,b ])
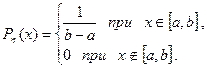
Применяя формулу композиции имеем.
,
делая замену в интеграле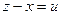 
, получаем
.
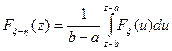Поскольку 
, то мы получаем формулу для плотности:
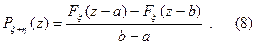
Пример 2. Рассмотрим частный случай примера 1, когда величины ξ и η равномерно распределены на отрезке [0,1]
, 
Тогда из формулы (8) получаем
График функции Pξ+η (z) показан на рисунке 2.
z
Замечание. Из формулы (5) можно также установить, что сумма независимых случайных величин, распределенных по нормальному закону, сама имеет нормальное распределение.
