Приведенные выше методы построения формул численного интегрирования одного дифференциального уравнения без всяких изменений переносятся на случай систем уравнений и уравнений высокого порядка.
Для уравнений высокого порядка необходимо перейти к нормальной форме Коши
,
и все рассмотренные выше операции выполняются над векторами.
Например, схема Эйлера выглядит следующим образом:
,
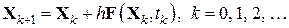или для элементов вектора 
в виде
.
Метод Рунге-Кутта 4-го порядка будет давать следующую вычислительную схему:
,
где
,
,
,
.
Для элементов вектора соответственно имеем
,
где
,
,
,
.
Вычислительные схемы, основанные на формулах Адамса, строятся аналогичным образом.
Основная проблема при решении уравнений высокого порядка – это переход к нормальной форме Коши. Если правая часть уравнения является укороченной, т.е. имеет место уравнение вида
,
то переход к нормальной форме является простым – вводятся новые переменные:
В этом случае нормальная форма Коши записи дифференциального уравнения будет выглядеть следующим образом:
Если правая часть не является укороченной, то есть имеет место уравнение вида:
,
то нормальная (каноническая) форма Коши будет иметь следующий вид:
(8.25)
где
, 
.
Как видим, для приведения уравнения 
-го порядка с переменными коэффициентами к канонической форме уравнений первого порядка необходимо, чтобы существовали производные от коэффициентов этого уравнения до 
-го порядка включительно.
Аналогичная процедура выполняется и для нелинейных уравнений.
Рассмотрим нелинейное уравнение второго порядка
,
где
– произвольная нелинейная функция.
Перейдем к нормальной форме Коши. Система уравнений в данном, частном случае, будет следующей
,
,
,
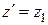Функции 
, 
, 
вычисляются согласно приведенным выше формулам, а именно:
,
,
.
Формула (8.25) в векторно-матричном виде выглядит следующим образом
, (8.26)
где
, (8.27)
,
, 
.
Рассмотрим реализацию неявного метода Адамса на примере формулы (8.24) для системы линейных уравнений (8.26).
Формула Адамса (8.24) для системы уравнений будет иметь вид
.
Подставляя в нее правые части уравнения (8.26), записанные в форме (8.27), будем иметь
.
Преобразуем данное уравнение относительно переменной 
:
(8.28)
Если ввести обозначения
,
,
выражение (8.28) приобретает вид
. (8.29)
Уравнение (8.29) представляет собой систему линейных алгебраических уравнений относительно искомого решения . Решение последнего находится в виде
.
Как видим, при реализации неявных методов, построенных по схеме Адамса, на каждом шаге интегрирования приходится решать систему линейных алгебраических уравнений.
Для повышения сходимости вычислительных схем рекомендуется использовать малый шаг интегрирования 
.
[1] «В среднем» здесь понимается в вероятностном смысле.
[2] Имеется более общее определение числа обусловленности:
Здесь задается через векторные нормы и может быть применено к вырожденным матрицам. В случае обратимых матриц при использовании согласованных матричных норм отсюда получается.
* от англ. Successive over relaxation
* В зарубежной литературе используется аббревиатура ADI- Alternating Direction Implicite
* Полагая,видим, что, в силу 2.3 и 2.1,.
* Через здесь обозначается спектральный радиус указанной вскобках матрицы
* Здесь и далее под дифференцируемостью понимается дифференцируемость по Фреше (см. приложение 1).
** т.е. на множестве точек таких, что.
