Если матрица 
мала (в смысле ее нормы или собственных значений), то обратная к 
матрица
,
в принципе, может быть найдена сколь угодно точно приближенным суммированием данного матричного ряда. Однако такой непосредственный подход к вычислению имеет два очевидных недостатка: во-первых, реально его можно применить лишь для обращения матриц, близких к единичной, во-вторых, сходимость последовательностей частичных сумм этого ряда будет медленной даже при достаточно малых нормах матриц 
. Поэтому, пользуясь отмеченным фактом лишь как теоретической основой, построим итерационный процесс, определяющий существенно более быстро сходящуюся последовательность приближений к обратной для матрице 
. Будем далее обозначать эти приближения, получаемые на 
-м шаге, через 
, а их невязки 
– через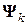 
.
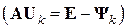Лемма 6.3. Если для матрицы найдется такая обратимая матрица 
, что модули всех собственных чисел матрицы 
меньше единицы, то матрица обратима и для обратной матрицы справедливо представление
(6.31)
Лемма 6.4. Пусть матрица обратима и 
.
Тогда:
1) существует матрица ;
2) справедливо представление по формуле (6.31);
3) имеет место оценка 
Для построения итерационного процесса зафиксируем в разложении (6.31) 
первых слагаемых и будем считать первым приближением к матрицу
Найдем выражение невязки 
этого приближения через невязку 
предыдущего (в данном случае начального) приближения :
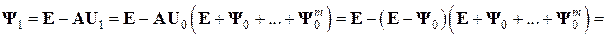
(6.33)
Благодаря полученной связи между невязками, можно утверждать, что если выполняются условия лемм 6.3 или 6.4 по отношению к матрицам , , то для матриц 
, они тем более будут выполнены. Следовательно, к матрицам , , можно применить все рассуждения, проведенные выше для , . Таким образом, приходим к итерационному процессу
(6.34)
где 
– номер итерации; – задаваемая начальная матрица, близкая к в указанном выше смысле, а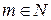 
– параметр метода.
Теорема 6.13. Пусть квадратные матрицы и таковы, что матрица обратима и . Тогда существует обратная к матрица и к ней сходится последовательность матриц , определяемая итерационным процессом (6.34). При этом имеет место точное равенство
и справедливы оценки погрешности:
1) 
;
2) 
.
Равенства (6.34) определяют фактически не один, а целое семейство итерационных методов обращения. Фиксированием параметра 
можно получать конкретные процессы 
-го порядка скорости сходимости. Этот порядок может быть сколь угодно большим, однако обычно ограничиваются процессами второго 
и третьего 
порядков. Приоритет процесса второго порядка связан с его простотой и более ранним появлением: первая публикация об этом методе относится к 1933 г. и принадлежит Г. Шульцу, в связи с чем и все семейство (6.34) естественно называть методом Шульца. Метод третьего порядка целесообразно использовать из тех соображений, что он, как показал М. Альтман, обладает свойством минимальности вычислительных затрат, требующихся для обращения матриц с заданной точностью методами семейства (6.34).
Процесс (6.34) построения приближений к обратной матрице легко видоизменить подобно тому, как это было сделано с методом простых итераций решения СЛАУ, когда для более оперативного учета получаемой на текущей итерации информации перешли от него к методу Зейделя (см. прарграф 6.3). Например, зейделева модификация метода Шульца второго порядка может быть определена равенствами
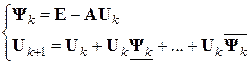, (6.40)
где ; 
; 
и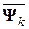 
– соответственно нижняя треугольная и строго верхняя треугольная матрицы. При реализации этой модификации нужно либо расписывать формулы (6.40) поэлементно (чтобы не работать с заведомо нулевыми элементами), либо формировать матрицу 
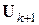постепенным замещением старых элементов новыми, осуществляя на -й итерации цикл присвоений
,
где до начала цикла в правой части в двумерном массиве 
должна содержаться матрица , а в двумерном массиве 
матрица 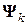(заполнение массивов новыми элементами производится по строкам). Процесс (6.40) при том же шаговом объеме вычислений и такой же простоте, что и в методе Шульца второго порядка, может дать определенный выигрыш в скорости сходимости.
Вообще, проблема выбора начального приближения в рассматриваемых здесь процессах, итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующим с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору , обеспечивающие выполнение условия* 
, являющегося необходимым и достаточным для сходимости процесса (6.34). Однако при этом, во-первых, требуется знать оценку сверху спектра обращаемой матрицы либо матрицы 
(а именно, если, – симметричная положительно определенная и 
, то можно взять 
, где 
; если же произвольная невырожденная матрица и 
, то полагают 
, где также ; можно, конечно, упростить ситуацию и, воспользовавшись тем, что 
, положить 
). Во-вторых, при таком задании начальной матрицы нет гарантии, что 
будет малой (возможно, даже окажется 
), и высокий порядок скорости сходимости обнаружится далеко не сразу.
Все сказанное выше не означает, что подобные методы обращения матриц (и операторов) не имеют своей сферы применения. В частности, ниже будет рассматриваться способ решения систем нелинейных уравнений, базирующиеся на методе Ньютона с приближенным обращением матриц Якоби по методу Шульца, а в также метод Шульца используется как составная часть квадратурно-итерационного метода вычисления резольвент линейных интегральных уравнений.
